高中数学数列综合解答题

已知{a_n}为等差数列，且a₃＝－6，a₆＝0．
（1）求{a_n}的通项公式；
（2）若等比数列{b_n}满足b₁＝－8，b₂＝a₁＋a₂＋a₃，求{b_n}的前n项和．

（本小题满分16分）
已知数列是等差数列，是等比数列，且满足，．
（1）若，．
①当时，求数列和的通项公式；
②若数列是唯一的，求的值；
（2）若，，均为正整数，且成等比数列，求数列的公差的最大值．

（本小题满分12分）已知等差数列满足=2，前3项和=．
（Ⅰ）求的通项公式，
（Ⅱ）设等比数列满足=，=，求前n项和．

已知等差数列满足=2，前3项和=．
（1）求的通项公式；
（2）设等比数列满足=，=，求前n项和．

（本小题满分12分）在正项等比数列中，已知，．
（1）求数列的通项公式；
（2）若，,求证：数列是等差数列；
（3）设数列满足的前项和．

已知数列{a_n}满足a₁="3" 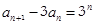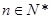，（），数列{b_n}满足．
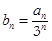（1）证明数列{b_n}是等差数列并求数列{b_n}的通项公式；
（2）求数列{a _n}的前n项和S _n．

已知数列是公差不为的等差数列,,且,,成等比数列．
（1）求数列的通项公式；
（2）设,求数列的前项和．

已知等差数列{a_n}满足a₂＝2，a₅＝8．
（1）求{a_n}的通项公式；
（2）各项均为正数的等比数列{b_n}中，b₁＝1，b₂＋b₃＝a₄，求{b_n}的前n项和T_n．

已知数列满足，．
（Ⅰ）求证：是等差数列；
（Ⅱ）证明：．

（本小题满分12分）已知是等差数列的前项和，满足；是数列的前项和，满足：。
（1）求数列，的通项公式；
（2）求数列的前项和

等差数列中,
（1）求的通项公式;
（2）设

（本小题满分12分）等差数列的前项和为，数列是等比数列，满足．
（Ⅰ）求数列和的通项公式；
（Ⅱ）设，求数列的前项和．

在△ABC中，角A，B，C的对应边分别是a，b，c满足b²+c²=bc+a²．
（Ⅰ）求角A的大小；
（Ⅱ）已知等差数列{a_n}的公差不为零，若a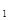cosA=1，且a ₂ ，a ₄ ，a ₈成等比数列，求{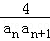}的前n项和S_n．

（本小题满分10分）中，分别为角所对的边．
（Ⅰ）若成等差数列，求的值；
（Ⅱ）若成等比数列，求角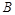的取值范围．

（本小题满分12分）已知数列满足，，令.
（Ⅰ）证明：数列是等差数列；
（Ⅱ）求数列的通项公式．