高中数学数列综合解答题

等差数列中，，公差为整数，若，．
(2)求前项和的最大值；

已知等差数列满足：，，的前n项和为．
（Ⅰ）求及；
（Ⅱ）令b_n=(nN^*)，求数列的前n项和．

（本小题满分13分）设数列是首项为，公差为的等差数列，且是等比数列的前三项.
（1）求的通项公式；
（2）求数列的前项和.

(本题满分12分)数列的前项的和为,对于任意的自然数，
（Ⅰ）求证：数列是等差数列，并求通项公式
（Ⅱ）设，求和

设等差数列{}的前项和为，已知＝，．
(Ⅰ) 求数列{}的通项公式；
（Ⅱ）求数列{}的前n项和；
（Ⅲ）当n为何值时，最大，并求的最大值．

等差数列中，且成等比数列，求数列前20项的和．

已知数列满足，．
（Ⅰ）求证：是等差数列；
（Ⅱ）证明：．

已知 是等差数列，是公比为的等比数列，，记为数列的前项和，
（1）若是大于的正整数，求证：；
（2）若是某一正整数，求证：是整数，且数列中每一项都是数列中的项；
（3）是否存在这样的正数，使等比数列中有三项成等差数列？若存在，写出一个的值，并加以说明；若不存在，请说明理由；

各项均为正数的等差数列首项为1，且成等比数列，
（1）求、通项公式；
（2）求数列前n项和；
（3）若对任意正整数n都有成立，求范围.

等差数列中,
（1）求的通项公式;
（2）设

在△ABC中，角A，B，C的对应边分别是a，b，c满足b²+c²=bc+a²．
（Ⅰ）求角A的大小；
（Ⅱ）已知等差数列{a_n}的公差不为零，若acosA=1，且a ₂ ，a ₄ ，a ₈成等比数列，求{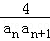}的前n项和S_n．

（本小题满分10分）中，分别为角所对的边．
（Ⅰ）若成等差数列，求的值；
（Ⅱ）若成等比数列，求角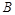的取值范围．

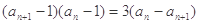（本小题满分12分）已知数列满足，，令.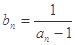
（Ⅰ）证明：数列是等差数列；
（Ⅱ）求数列的通项公式．

已知公比不为的等比数列的首项，前项和为，且成等差数列．
（1）求等比数列的通项公式；
（2）对，在与之间插入个数，使这个数成等差数列，记插入的这个数的和为，求数列的前项和．

已知是等差数列，其前项和为，已知
（1）求数列的通项公式；
（2）设，证明:是等比数列，并求其前项和.
(3) 设,求其前项和