高中数学数列综合解答题

已知等差数列的前项和为，．
（1）求数列的通项公式；
（2）求数列的前项和为

已知数列的前n项和和通项满足，等差数列中，.
（1）求数列，的通项公式；
（2）数列满足，求证：.

已知等差数列的各项互不相等，前两项的和为10，设向量，且．
（1）求数列的通项公式；
（2）若的前项和为，求证：

设是公比大于1的等比数列，为数列的前项和．已知，且构成等差数列．
（1）求数列的通项公式．
（2）令求数列的前项和．

已知各项均为正数的数列前n项和为，首项为，且成等差数列。
（1）求数列的通项公式；
（2）若，设，求数列的前n项和．

数列满足，，．
（1）证明：数列是等差数列；
（2）设，求数列的前项和．

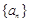在数列中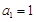，，且对任意的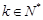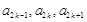，成等比数列，其公比为．
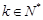（1）若=2（），求；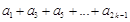
（2）若对任意的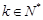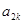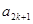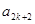，，，成等差数列，其公差为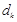，设．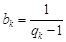
① 求证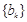：成等差数列，并指出其公差；
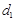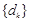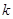② 若=2，试求数列的前项的和．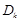

已知等差数列{a_n}的前n项和为S_n，且满足a₂=4，a₃+a₄=17．
（1）求{a_n}的通项公式；
（2）设b_n=2^an+2，证明数列{b_n}是等比数列并求其前n项和T_n．

数列为公差不为的等差数列，为前项和，和的等差中项为，且．令数列的前项和为．
（Ⅰ）求及；
（Ⅱ）是否存在正整数成等比数列？若存在，求出所有的的值；若不存在，请说明理由．

已知公差不为0的等差数列的前项和为，若，且成等比数列
（1）求的通项公式；
（2）设，求数列的前项和为．

在数列{a_n}中，a₁=1，a_n+1=2a_n+2ⁿ．
（1）设b_n=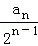，证明：数列{bn}是等差数列；
（2）求数列{a_n}的前n项和S_n，
（3）设c_n=，求数列{c_n}的最大项．

已知两个动点、和一个定点均在抛物线上（、与不重合）. 设为抛物线的焦点，为其对称轴上一点，若，且、、成等差数列.
（Ⅰ）求的坐标（可用、和表示）；
（Ⅱ）若，，、两点在抛物线的准线上的射影分别为、，求四边形面积的取值范围.

已知公差不为零的等差数列{a_n}，若a₁=1，且a₁，a₂，a₅成等比数列．
（1）求数列{a_n}的通项公式；
（2）设b_n=2ⁿ，求数列{a_n+b_n}的前n项和S_n．

已知数列的前项和为，且满足．
（1）求数列的通项公式;
（2）若，，且数列的前项和为，求的取值范围．

设数列满足：.
（Ⅰ）求证：数列是等比数列；
（Ⅱ）若，且对任意的正整数，都有，求实数的取值范围.