已知两个动点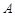 、
、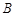 和一个定点
和一个定点 均在抛物线
均在抛物线 上(
上(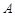 、
、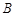 与
与 不重合). 设
不重合). 设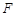 为抛物线的焦点,
为抛物线的焦点,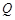 为其对称轴上一点,若
为其对称轴上一点,若 ,且
,且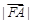 、
、 、
、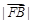 成等差数列.
成等差数列.
(Ⅰ)求 的坐标(可用
的坐标(可用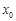 、
、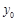 和
和 表示);
表示);
(Ⅱ)若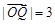 ,
, ,
,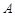 、
、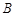 两点在抛物线
两点在抛物线 的准线上的射影分别为
的准线上的射影分别为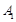 、
、 ,求四边形
,求四边形 面积的取值范围.
面积的取值范围.
推荐套卷
已知两个动点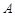 、
、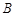 和一个定点
和一个定点 均在抛物线
均在抛物线 上(
上(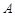 、
、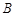 与
与 不重合). 设
不重合). 设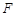 为抛物线的焦点,
为抛物线的焦点,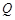 为其对称轴上一点,若
为其对称轴上一点,若 ,且
,且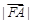 、
、 、
、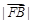 成等差数列.
成等差数列.
(Ⅰ)求 的坐标(可用
的坐标(可用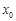 、
、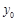 和
和 表示);
表示);
(Ⅱ)若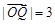 ,
, ,
,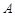 、
、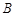 两点在抛物线
两点在抛物线 的准线上的射影分别为
的准线上的射影分别为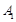 、
、 ,求四边形
,求四边形 面积的取值范围.
面积的取值范围.