(本小题满分13分)已知数列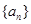 满足
满足 ,
, 为其前
为其前 项和,且
项和,且 .
.
(1)求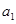 的值;
的值;
(2)求证: ;
;
(3)判断数列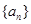 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
(本小题满分12分)已知数列 满足
满足 ,
, (
( ).
).
(Ⅰ)证明:数列 是等差数列;
是等差数列;
(Ⅱ)设 ,数列
,数列 的前
的前 项和
项和 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知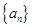 ,
,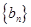 ,
, 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足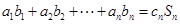 ,
,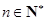 ,其中
,其中 是数列
是数列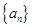 的前
的前 项和,
项和,  是公差为
是公差为 的等差数列.
的等差数列.
(1)若数列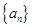 是常数列,
是常数列,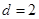 ,
,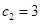 ,求数列
,求数列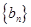 的通项公式;
的通项公式;
(2)若 (
( 是不为零的常数),求证:数列
是不为零的常数),求证:数列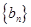 是等差数列;
是等差数列;
(3)若 (
(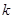 为常数,
为常数,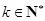 ),
),
 ,求证:对任意的
,求证:对任意的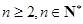 ,数列
,数列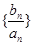 单调递减.
单调递减.
(本小题满分12分)已知等差数列 ,
, 为其前
为其前 项和,
项和,
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和
(本小题满分12分)已知数列 是公差不为
是公差不为 的等差数列,
的等差数列,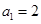 ,且
,且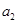 ,
, ,
,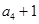 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列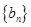 的前
的前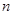 项和
项和 .
.
(本小题满分10分)等差数列 中,
中, ,公差
,公差 且
且 成等比数列,前
成等比数列,前 项的和为
项的和为 .
.
(1)求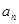 及
及 ;
;
(2)设 ,
,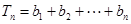 ,求
,求 .
.
(本小题满分13分)已知数列 满足
满足 ,
, 为其前
为其前 项和,且
项和,且 .
.
(1)求 的值;
的值;
(2)求证: ;
;
(3)判断数列 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
(本小题满分13分)设数列 是首项为
是首项为 ,公差为
,公差为 的等差数列,且
的等差数列,且 是等比数列
是等比数列 的前三项.
的前三项.
(1)求 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
已知等差数列{an}满足a3=5,a5﹣2a2=3,又等比数列{bn}中,b1=3且公比q=3.
(1)求数列{an},{bn}的通项公式;
(2)若cn=an+bn,求数列{cn}的前n项和Sn.
已知等差数列{an}中,a1=1,a3=-3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-35,求k的值.
已知首项为 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn- (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.