已知首项为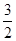
的等比数列{an}不是递减数列，其前n项和为Sn(n∈N*)，且S3＋a3，S5＋a5，S4＋a4成等差数列．
(1)求数列{an}的通项公式；
(2)设Tn＝Sn－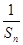
(n∈N*)，求数列{Tn}的最大项的值与最小项的值．
相关试题
. 
的值．
的解集为
．
；
．
．
的最大值．
的前
项和为
，常数
，且
对一切正整数
，
，求证： 
<4
的最大值.推荐套卷
已知首项为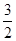的等比数列{an}不是递减数列，其前n项和为Sn(n∈N*)，且S3＋a3，S5＋a5，S4＋a4成等差数列．
(1)求数列{an}的通项公式；
(2)设Tn＝Sn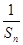－ (n∈N*)，求数列{Tn}的最大项的值与最小项的值．
粤公网安备 44130202000953号