(本小题16分)已知等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,公差
,公差 .
.
(1)若 成等比数列,求数列
成等比数列,求数列 的通项公式;
的通项公式;
(2)是否存在数列 ,使得对任意的
,使得对任意的 ,
, 仍然是数列
仍然是数列 中的一项?若存在,求出所有满足条件的公差
中的一项?若存在,求出所有满足条件的公差 ;若不存在,说明理由;
;若不存在,说明理由;
(3)设数列 的每一列都是正整数,且
的每一列都是正整数,且 ,若数列
,若数列 是等比数列,求数列
是等比数列,求数列 的通项公式.
的通项公式.
设数列 的前
的前 项和为
项和为 .若对任意的正整数
.若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得 ,则称
,则称 是“
是“ 数列”.
数列”.
(1)若数列 的前
的前 项和为
项和为 ,证明:数列
,证明:数列 是“
是“ 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差 ,若
,若 是“
是“ 数列”,求
数列”,求 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“ 数列”
数列” 和
和 ,使得
,使得
 成立.
成立.
(本小题12分)数列 首项
首项 ,前
,前 项和
项和 与
与 之间满足
之间满足
(1)求证:数列 是等差数列
是等差数列
(2)求数列 的通项公式
的通项公式
(3)设存在正数 ,使
,使 对于一切
对于一切 都成立,求
都成立,求 的最大值.
的最大值.
已知数列{an}的前n项和Sn满足 ,
,
(1)求数列{an}的通项公式;
(2)求证:数列{an}中的任意三项不可能成等差数列;
(3)设 ,Tn为{bn}的前n项和,求证
,Tn为{bn}的前n项和,求证 .
.
(本小题满分8分)
设等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分14分)已知等差数列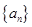 中,
中,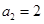 ,
, ,各项为正数的等比数列
,各项为正数的等比数列 中,
中, ,
,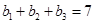 .
.
(1)求数列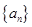 和
和 的通项公式;
的通项公式;
(2)若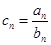 ,求数列
,求数列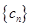 的前
的前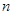 项和
项和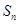 .
.
(本小题满分12分)
(Ⅰ)已知等差数列 ,
, ,求证:
,求证: 仍然为等差数列;
仍然为等差数列;
(Ⅱ)已知等比数列 ,
, ,类比上述性质,写出命题并证明.
,类比上述性质,写出命题并证明.
(本小题满分12分)数列 的前n项和记为
的前n项和记为  ,等差数列
,等差数列 的各项为正,其前n项和为
的各项为正,其前n项和为 ,且
,且 ,又
,又  成等比数列.
成等比数列.
(Ⅰ)求  ,
, 的通项公式;
的通项公式;
(Ⅱ)求证:当n  2时,
2时,