高中数学试题

如图，在中，，斜边．可以通过 以直线为轴旋转得到，且二面角是直二面角．动点在斜边上．

（1）求证：平面平面；
（2）求与平面所成角的最大角的正切值．

如图，在四棱锥中，底面是正方形，侧棱⊥底面，，是的中点，作交于点．

（1）证明平面；
（2）证明平面．

在直三棱柱中,,，求：

（1）异面直线与所成角的余弦值；
（2）直线到平面的距离．

将正方形沿对角线折成直二面角，有如下四个结论：
①⊥;②△是等边三角形;③与平面所成的角为60°;
④与所成的角为60°.其中错误的结论是

A．①

B．②

C．③

D．④

已知函数，函数是区间上的减函数.
（1）求的最大值；
（2）若恒成立，求的取值范围；
(3）讨论关于的方程的根的个数．

定义在定义域内的函数，若对任意的都有，则称函数为“妈祖函数”，否则称“非妈祖函数”.试问函数,（)是否为“妈祖函数”？如果是，请给出证明；如果不是，请说明理由.

已知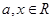函数,函数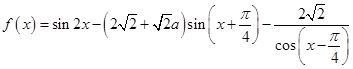
⑴当时,求函数的表达式;
⑵若,函数在上的最小值是2 ,求的值.

已知
（1）求的单调增区间
（2）若在内单调递增，求的取值范围.

设函数是定义在上的函数，其中的导函数为，满足对于恒成立，则

A．	B．
C．	D．

已知，函数.
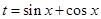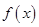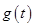（1）设，将函数表示为关于的函数，求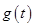的解析式和定义域；
（2）对任意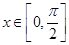，不等式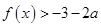都成立，求实数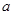的取值范围.

如图所示，某市政府决定在以政府大楼为中心，正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地，并考虑与周边环境协调，设计要求该图书馆底面矩形的四个顶点都要在边界上，图书馆的正面要朝市政府大楼.设扇形的半径 ，，与之间的夹角为.

（1）将图书馆底面矩形的面积表示成的函数.
（2）求当为何值时，矩形的面积有最大值？其最大值是多少？(用含R的式子表示)

设平面向量＝，，，，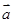
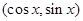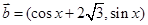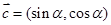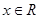⑴若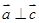，求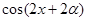的值；（2）若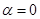，求函数的最大值，并求出相应的值．

如图，是圆的直径,点是圆上异于的点，直线 分别为的中点。

（1）记平面与平面的交线为，试判断与平面的位置关系，并加以说明；
（2）设（1）中的直线与圆的另一个交点为，且点满足，记直线
平面所成的角为异面直线与所成的锐角为，二面角的大小为
①求证：
②当点为弧的中点时，，求直线与平面所成的角的正弦值。

如图，在等腰直角三角形中， =90⁰ ，="6," 分别是，上的点，  为的中点.将沿折起，得到如图所示的四棱椎，其中

（1）证明：；
（2）求二面角的平面角的余弦值.

如图所示，在三棱柱中，，，点分别是的中点．
 
(1)求证：平面∥平面；
(2)求证：平面⊥平面；
（3）若，，求异面直线所成的角。