已知函数
(1)求函数 的单调区间.
的单调区间.
(2)若方程 有4个不同的实根,求
有4个不同的实根,求 的范围?
的范围?
(3)是否存在正数 ,使得关于
,使得关于 的方程
的方程 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由.
在平面直角坐标系中,已知三点 ,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为
,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为 ,而直线AB恰好经过抛物线
,而直线AB恰好经过抛物线 )的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则
)的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则 ( )
( )
| A.9 | B. |
C. |
D. |
已知两座灯塔A、B与C的距离都是a,灯塔A在C的北偏东20°,灯塔B在C的南偏东40°,则灯塔A与灯塔B的距离为 ( )
| A.a | B. |
C. |
D.2a |
已知函数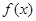 的定义域[-1,5],部分对应值如表,
的定义域[-1,5],部分对应值如表,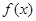 的导函数
的导函数 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数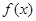 的命题;
的命题;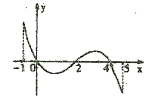
| x |
-1 |
0 |
2 |
4 |
5 |
| F(x) |
1 |
2 |
1.5 |
2 |
1 |
①函数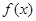 的值域为[1,2];
的值域为[1,2];
②函数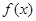 在[0,2]上是减函数;
在[0,2]上是减函数;
③如果当 时,
时,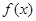 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
④当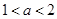 时,函数
时,函数 最多有4个零点.
最多有4个零点.
其中正确命题的序号是 .
已知函数 下列结论中①
下列结论中① ②函数
②函数 的图象是中心对称图形 ③若
的图象是中心对称图形 ③若 是
是 的极小值点,则
的极小值点,则 在区间
在区间 单调递减 ④若
单调递减 ④若 是
是 的极值点,则
的极值点,则 . 正确的个数有( )
. 正确的个数有( )
| A.1 | B.2 | C.3 | D.4 |
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
如图, 是圆
是圆 的直径,
的直径, 是
是 延长线上的一点,
延长线上的一点, 是圆
是圆 的割线,过点
的割线,过点 作
作 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线  于点
于点 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 .
.
(1)求证: 四点共圆;(2)若
四点共圆;(2)若 ,求
,求 的长.
的长.
如图,已知四棱锥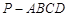 ,底面
,底面 是等腰梯形,且
是等腰梯形,且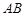 ∥
∥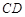 ,
,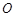 是
是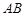 中点,
中点,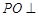 平面
平面 ,
,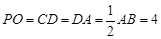 ,
, 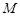 是
是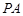 中点.
中点.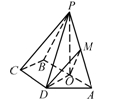
(1)证明:平面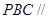 平面
平面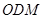 ;(2)求点
;(2)求点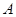 到平面
到平面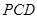 的距离.
的距离.
设函数 是定义在
是定义在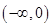 上的可导函数,其导函数为
上的可导函数,其导函数为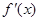 ,且有
,且有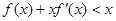 ,则不等式
,则不等式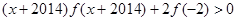 的解集为( )
的解集为( )
A.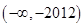 |
B.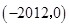 |
C.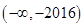 |
D.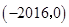 |
已知命题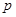 :函数
:函数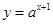 的图象恒过定点
的图象恒过定点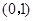 ;命题
;命题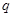 :若函数
:若函数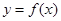 为偶函数,则函数
为偶函数,则函数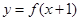 的图像关于直线
的图像关于直线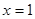 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )
A.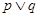 |
B. |
C.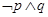 |
D.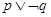 |
设函数 .
.
(1)若不等式 的解集为
的解集为 ,求
,求 的值;
的值;
(2)若存在 ,使
,使 ,求
,求 的取值范围.
的取值范围.