吉林省长春市高中毕业班第二次调研测试文科数学试卷
已知命题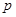 :函数
:函数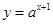 的图象恒过定点
的图象恒过定点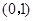 ;命题
;命题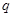 :若函数
:若函数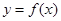 为偶函数,则函数
为偶函数,则函数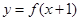 的图像关于直线
的图像关于直线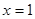 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )
A.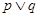 |
B. |
C.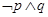 |
D.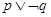 |
以下四个命题:
①从匀速传递的产品生产流水线上,质检员每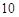 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个变量的线性相关性越强,则它们的相关系数的绝对值越接近于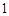 ;
;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
④对分类变量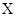 与
与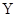 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“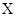 与
与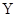 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
| A.①④ | B.②④ | C.①③ | D.②③ |
已知直线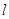 与双曲线
与双曲线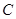 交于
交于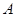 ,
,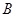 两点(
两点(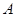 ,
,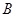 不在同一支上),
不在同一支上),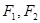 为双曲线的两个焦点,则
为双曲线的两个焦点,则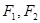 在( )
在( )
A.以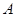 , ,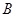 为焦点的双曲线上 为焦点的双曲线上 |
B.以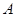 , ,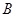 为焦点的椭圆上 为焦点的椭圆上 |
C.以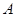 , ,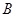 为直径两端点的圆上 为直径两端点的圆上 |
D.以上说法均不正确 |
设函数 是定义在
是定义在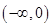 上的可导函数,其导函数为
上的可导函数,其导函数为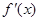 ,且有
,且有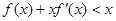 ,则不等式
,则不等式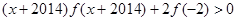 的解集为( )
的解集为( )
A.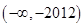 |
B.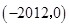 |
C.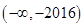 |
D.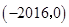 |
如图,在长方体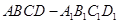 中,
中,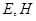 分别是棱
分别是棱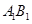 ,
,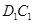 上的点(点
上的点(点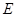 与
与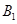 不重合),且
不重合),且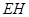 ∥
∥ ,过
,过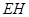 的平面与棱
的平面与棱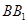 ,
,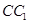 相交,交点分别为
相交,交点分别为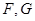 .设
.设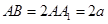 ,
,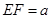 ,
,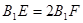 .在长方体
.在长方体 内随机选取一点,则该点取自于几何体
内随机选取一点,则该点取自于几何体 内的概率为 .
内的概率为 .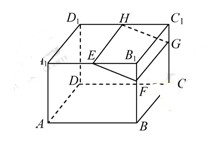
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.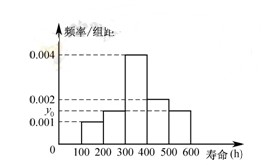
(1)求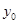 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取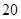 个元件,元件寿命落在
个元件,元件寿命落在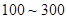 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在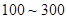 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在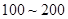 之间,一个元件寿命落在
之间,一个元件寿命落在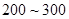 之间”的概率.
之间”的概率.
如图,已知四棱锥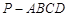 ,底面
,底面 是等腰梯形,且
是等腰梯形,且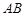 ∥
∥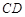 ,
,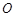 是
是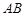 中点,
中点,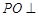 平面
平面 ,
,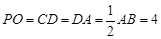 ,
, 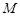 是
是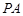 中点.
中点.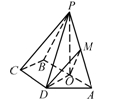
(1)证明:平面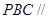 平面
平面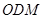 ;(2)求点
;(2)求点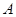 到平面
到平面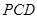 的距离.
的距离.
如图,已知点 是离心率为
是离心率为 的椭圆
的椭圆 :
:
 上的一点,斜率为
上的一点,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 ,
, 两点,且
两点,且 、
、 、
、 三点互不重合.
三点互不重合.
(1)求椭圆 的方程;(2)求证:直线
的方程;(2)求证:直线 ,
, 的斜率之和为定值.
的斜率之和为定值.
如图, 是圆
是圆 的直径,
的直径, 是
是 延长线上的一点,
延长线上的一点, 是圆
是圆 的割线,过点
的割线,过点 作
作 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线  于点
于点 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 .
.
(1)求证: 四点共圆;(2)若
四点共圆;(2)若 ,求
,求 的长.
的长.
已知直线 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)若 是直线
是直线 与圆面
与圆面 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围.
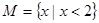 ,集合
,集合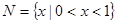 ,则下列关系中正确的是( )
,则下列关系中正确的是( )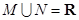
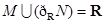
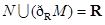
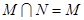
 是虚数单位,则
是虚数单位,则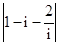 等于( )
等于( )

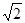
 ,
,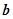
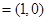 ,
,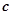
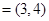 ,若
,若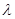 为实数,
为实数,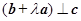 ,则
,则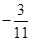
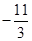
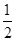
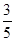
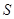 是
是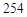 ,则①应为( )
,则①应为( )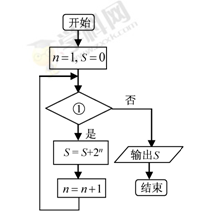
 ≤
≤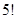
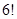
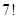
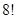
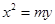
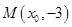 到焦点的距离为
到焦点的距离为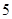 ,则实数
,则实数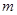 的值为( )
的值为( )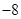
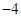
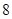
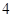
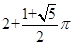
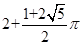
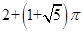

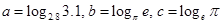 ,则( )
,则( )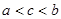
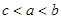
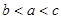
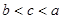
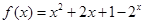 ,则
,则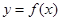 的图象大致为( )
的图象大致为( )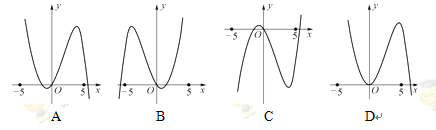
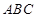 中,三个内角
中,三个内角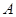 ,
,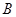 ,
,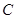 所对的边分别为
所对的边分别为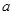 ,
,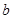 ,
,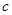 ,若
,若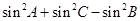
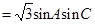 ,则
,则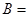 .
.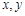 满足约束条件
满足约束条件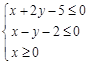 ,则目标函数
,则目标函数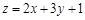 的最大值为 .
的最大值为 .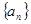 中,
中,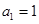 ,
, 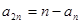 ,
,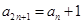 ,则
,则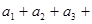
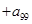 = .
= .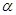 为锐角,且
为锐角,且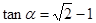 ,函数
,函数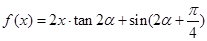 ,数列
,数列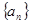 的首项
的首项 ,
,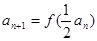 .
.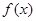 的表达式;(2)求数列
的表达式;(2)求数列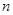 项和
项和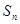 .
. 在
在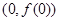 处切线为
处切线为 .
. 的解析式;
的解析式; ,
, ,
, ,
, 表示直线
表示直线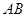 的斜率,求证:
的斜率,求证: .
. .
. 的解集为
的解集为 ,求
,求 的值;
的值; ,使
,使 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号