(本小题满分12分)
已知在椭圆
 中,
中, 分别为椭圆的左右焦点,直线
分别为椭圆的左右焦点,直线 过椭圆
过椭圆 右焦点
右焦点 ,且与椭圆的交点为
,且与椭圆的交点为 (点
(点 在第一象限),若
在第一象限),若 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)以 为圆心的动圆与
为圆心的动圆与 轴分别交于两点A、B,延长
轴分别交于两点A、B,延长 ,分别交椭圆
,分别交椭圆 于
于 两点,判断直线
两点,判断直线 的斜率是否为定值,并说明理由.
的斜率是否为定值,并说明理由.
(本小题满分12分)
已知 三个内角
三个内角 的对边分别为
的对边分别为 ,
,
 的图象与直线
的图象与直线 相切,且切点横坐标依次成公差为
相切,且切点横坐标依次成公差为 的等差数列,点
的等差数列,点 是函数
是函数 的一个对称中心.
的一个对称中心.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)已知 ,
, 为
为 的面积,求
的面积,求 的最大值及此时B的值.
的最大值及此时B的值.
设函数 ,下列命题:
,下列命题:
①若 , 则
, 则 ;
;
②存在 ,
, ,使得
,使得 ;
;
③若 ,则
,则 ;
;
④对任意的 ,
, ,都有
,都有
其中正确的是_______________.(填写序号)
已知函数 ,若存在实数
,若存在实数 、
、 、
、 、
、 ,满足
,满足
 ,其中
,其中 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知焦点在 轴的椭圆
轴的椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,直线
,直线 过右焦点
过右焦点 ,和椭圆交于
,和椭圆交于 两点,且满足
两点,且满足 ,
,  ,则椭圆
,则椭圆 的标准方程为( )
的标准方程为( )
A. |
B. |
C. |
D. |
(本小题满分13分)
抛物线 上一点
上一点 到其焦点的距离为5.
到其焦点的距离为5.
(I)求 与
与 的值;
的值;
(II)若直线 与抛物线
与抛物线 相交于
相交于 、
、 两点,
两点, 、
、 分别是该抛物线在
分别是该抛物线在 、
、 两点处的切线,
两点处的切线, 、
、 分别是
分别是 、
、 与该抛物线的准线交点,求证:
与该抛物线的准线交点,求证: .
.
(本小题满分13分)已知函数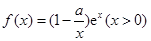 ,其中
,其中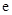 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当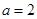 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积;
(Ⅱ)若函数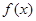 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为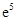 ,求
,求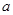 的值.
的值.
给出下列四个命题:
①命题“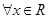 ,
, ”的否定是“
”的否定是“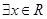 ,
, ”;
”;
②已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是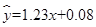 ;
;
③圆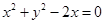 的圆心到直线
的圆心到直线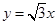 的距离是
的距离是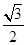 ;
;
④若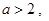 则方程
则方程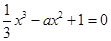 在
在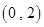 上恰好有1个根;
上恰好有1个根;
⑤对于大于1的自然数m的二次幂可以用技术进行以下方式的“分裂”: ……仿此,若
……仿此,若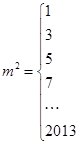 ,则m=1007;
,则m=1007;
其中真命题的序号是 .(填上所有真命题的序号)
将一副直角三角板如图摆放得四边形 ,再将四边形
,再将四边形 沿对角线
沿对角线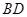 折成四面体
折成四面体 ,使平面
,使平面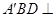 平面
平面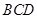 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )

A. |
B.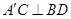 |
C.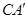 与平面 与平面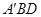 所成的角为 所成的角为 |
D.若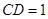 ,则四面体 ,则四面体 的体积为 的体积为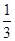 |
(本小题满分13分)已知数列 中,
中,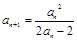 ,
,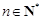 .
.
(Ⅰ)若 ,设
,设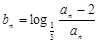 ,求证数列
,求证数列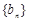 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
,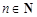 ,证明:
,证明: .
.
(本小题满分13分)已知椭圆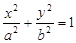 (
(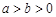 )的离心率为
)的离心率为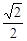 ,且短轴长为2.
,且短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)若与两坐标轴都不垂直的直线 与椭圆交于
与椭圆交于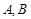 两点,
两点,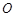 为坐标原点,且
为坐标原点,且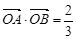 ,
, ,求直线
,求直线 的方程.
的方程.
已知函数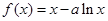 ,
,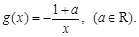
(Ⅰ)若 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数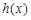 的单调区间;
的单调区间;
(Ⅲ)若在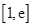 (
( )上存在一点
)上存在一点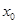 ,使得
,使得

 成立,求
成立,求 的取值范围.
的取值范围.
(本小题满分12分)如图多面体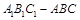 中,平面
中,平面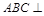 平面
平面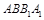 ,平面
,平面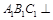 平面
平面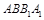 ,
,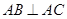 ,
, ,
,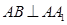 ,
, ,且
,且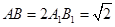 ,
,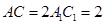 ,
,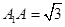 .
.

(Ⅰ)在BC上取一点D,当  为何值时,平面
为何值时,平面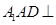 平面
平面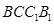 ;
;
(Ⅱ)求二面角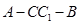 的余弦值.
的余弦值.
给出下列四个命题:
①命题“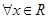 ,
, ”的否定是“
”的否定是“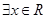 ,
,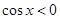 ”;
”;
②若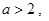 则方程
则方程 在
在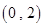 上恰好有1个根;
上恰好有1个根;
③如果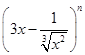 的展开式中二项式系数之和为128,则展开式中
的展开式中二项式系数之和为128,则展开式中 的系数是
的系数是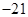 ;
;
④由直线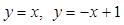 ,及x轴围成平面图形的面积为
,及x轴围成平面图形的面积为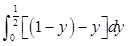 ;
;
其中真命题的序号是 .(填上所有真命题的序号)
如果一个 位十进制数
位十进制数 的数位上的数字满足“小大小大
的数位上的数字满足“小大小大 小大”的顺序,即满足:
小大”的顺序,即满足: ,我们称这种数为“波浪数”.从1,2,3,4,5组成的数字不重复的五位数中任取一个五位数
,我们称这种数为“波浪数”.从1,2,3,4,5组成的数字不重复的五位数中任取一个五位数 ,这个数为“波浪数”的概率是 ( )
,这个数为“波浪数”的概率是 ( )
A. |
B. |
C. |
D. |