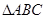高中数学试题

的内切圆与三边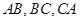的切点分别为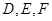,已知，内切圆圆心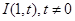,设点A的轨迹为R.

（1）求R的方程；
（2）过点C的动直线m交曲线R于不同的两点M,N，问在x轴上是否存在一定点Q（Q不与C重合），使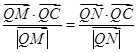恒成立，若求出Q点的坐标，若不存在，说明理由.

已知椭圆，圆，过椭圆上任一与顶点不重合的点P引圆O的两条切线，切点分别为A,B，直线AB与x轴,y轴分别交于点M,N，则_____________

菱形ABCD的边长为，,沿对角线AC折成如图所示的四面体，二面角B-AC-D为,M为AC的中点，P在线段DM上，记DP=x，PA+PB=y,则函数y=f(x)的图象大致为(    )

设等差数列的前项和为，且满足,则中最大的项为(    )

A．

B．

C．

D．

已知函数
（1）判断函数的奇偶性；
（2）试用函数单调性定义说明函数在区间和上的增减性；
（3）若满足：，试证明：．

函数的单调递减区间是      ．

设函数，则函数的零点的个数为(    )

A．4

B．7

C．6

D．无穷多个

如图所示，在△ABC中，点M是BC的中点，，点N在AC上，且AN＝2NC，AM与BN相交于点P，AP=λAM，求(1)λ的值   (2)

已知非零向量与满足(+)·=0且·= , 则△ABC为(     )

A．等腰直角三角形

B．直角三角形

C．等腰非等边三角形

D．等边三角形

已知函数
（1）求不等式的解集；
（2）若关于的不等式的解集非空，求实数的取值范围.

在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，过点的直线的参数方程为（为参数），直线与曲线相交于两点．
（1）写出曲线的直角坐标方程和直线的普通方程；
（2）若，求的值.

对于实数和，定义运算“”：，设，且关于的方程为恰有三个互不相等的实数根，则的取值范围是___________.

若函数对任意的恒成立，则      .

定义域为的函数满足当时，，若时， 恒成立，则实数的取值范围是（   ）

A．	B．
C．	D．

（满分12分）已知函数.
（1）当时，求函数的单调区间；
（2）若函数在区间上为减函数，求实数的取值范围；
（3）当时，不等式恒成立，求实数的取值范围.