一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为ξ,求ξ的分布列和数学期望Eξ;
(2)求恰好得到n(n∈N*)分的概率.
如图,已知三棱柱ABC—A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
(1)求证:PN⊥AM;
(2)若直线MB与平面PMN所成的角为θ,求sinθ的值.
选修44:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为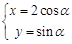 (α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为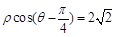 ,点P为曲线C上的动点,求点P到直线l距离的最大值.
,点P为曲线C上的动点,求点P到直线l距离的最大值.
选修42:矩阵与变换
已知矩阵M= 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1=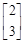 .
.
(1)求矩阵M;
(2)求曲线5x2+8xy+4y2=1在M的作用下的新曲线的方程.
选修41:几何证明选讲
如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.

(1)求证:OM·OP=OA2;
(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.求证:∠OKM=90°.
(本小题满分14分)在平面直角坐标系xOy中,如图,已知椭圆E: (a>b>0)的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为
(a>b>0)的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为 ,圆C与以线段OA2为直径的圆关于直线A1B1对称.
,圆C与以线段OA2为直径的圆关于直线A1B1对称.

(1)求椭圆E的离心率;
(2)判断直线A1B1与圆C的位置关系,并说明理由;
(3)若圆C的面积为π,求圆C的方程.
(本小题满分14分)已知函数 .
.
(1)设 ,且
,且 ,求θ的值;
,求θ的值;
(2)在△ABC中,AB=1, ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值.
,求sinA+sinB的值.
如图所示,在直三棱柱A1B1C1—ABC中,AC⊥BC,AC=4,BC=CC1=2.若用平行于三棱柱A1B1C1—ABC的某一侧面的平面去截此三棱柱,使得到的两个几何体能够拼接成长方体,则长方体表面积的最小值为________.
已知点A(0,2),抛物线y2=2px(p>0)的焦点为F,准线为l,线段FA交抛物线于点B,过B作l的垂线,垂足为M,若AM⊥MF,则p=__________.
在平面直角坐标系xOy中,已知A、B分别是双曲线 的左、右焦点,△ABC 的顶点C在双曲线的右支上,则
的左、右焦点,△ABC 的顶点C在双曲线的右支上,则 的值是____________.
的值是____________.
(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点 处,极轴与
处,极轴与 轴的正半轴重合,且长度单位相同。直线
轴的正半轴重合,且长度单位相同。直线 的极坐标方程为:
的极坐标方程为: ,点
,点 ,参数
,参数 .
.
(1)求点 轨迹的直角坐标方程;
轨迹的直角坐标方程;
(2)求点 到直线
到直线 距离的最大值.
距离的最大值.
(本小题满分10分)选修4-1:几何证明选讲
已知 中,
中, ,
, 是
是 外接圆劣弧
外接圆劣弧 上的点(不与点
上的点(不与点 重合),延长
重合),延长 至
至 。
。
(1)求证: 的延长线平分
的延长线平分 ;
;
(2)若 ,
, 中
中 边上的高为
边上的高为 ,求
,求 外接圆的面积。
外接圆的面积。