已知函数f(x)=﹣x3+ax2﹣x﹣1在(﹣∞,+∞)上是单调函数,则实数a的取值范围是
A. |
B. |
C. |
D. |
8名学生和2位老师站成一排合影,2位老师不相邻的排法种数为
A. |
B. |
C. |
D. |
(本小题满分13分)在四棱锥 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求证: 平面
平面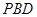 ;
;
(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)若 为第三象限角,且
为第三象限角,且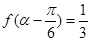 ,求
,求 的值.
的值.
各项都为正数的等比数列 中,
中, ,则
,则 的值为
的值为
A. |
B. |
C. |
D. |
(本题满分14分)已知函数 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为 .
.
(1)当 时,若不等式
时,若不等式 对任意
对任意
 恒成立,求b的取值范围;
恒成立,求b的取值范围;
(2)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线 ,关于x的方程
,关于x的方程 在
在 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.
如图,已知 ,
, 分别是正方形
分别是正方形 边
边 、
、 的中点,
的中点, 与
与 交于点
交于点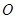 ,
, 、
、 都垂直于平面
都垂直于平面 ,且
,且 ,
, ,
, 是线段
是线段 上一动点.
上一动点.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若 平面
平面 ,试求
,试求 的值;
的值;
(Ⅲ)当 是
是 中点时,求二面角
中点时,求二面角 的余弦值.
的余弦值.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
(1)请根据图中所给数据,求出a的值;
(2)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.
数列
 是递增的等比数列,且
是递增的等比数列,且 .
.
(Ⅰ)若 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
(Ⅱ)若
 ,求
,求 的最大值.
的最大值.
在△ABC中, ,
, ,则△ABC的面积为( ).
,则△ABC的面积为( ).
A. |
B.3 | C. |
D.6 |
如图所示,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心)  的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于
的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于
A. |
B. |
C.12 | D.24 |
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数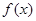 的极值;
的极值;
(Ⅱ)
 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅲ)若对任意的 恒有
恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)设平面向量 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 的单调递增区间.
的单调递增区间.