高中数学试题

已知两个正数a，b满足a+b=1
（1）求证：；
（2）若不等式对任意正数a，b都成立，求实数x的取值范围．

已知直线：（t为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的坐标方程为．
（1）将曲线C的极坐标方程化为直坐标方程；
（2）设点M的直角坐标为，直线l与曲线C的交点为A，B，求|MA|•|MB|的值．

已知ξ的分布列如下：

ξ	0	1	2
P

并且，则方差（ ）
A．           B．          C．           D．7

表中提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对应数据．根据下表提供的数据，求出y关于x的线性回归方程为=0.7x+0.35，那么表中t的值为（ ）

x	3	4	5	6
y	2.5	t	4	4.5

A．3           B．3.15           C．3.5           D．4.5

（本小题满分13分）已知函数，其中.
（Ⅰ）求函数的单调区间；
（Ⅱ）证明函数只有一个零点.

（本小题满分13分）设函数的定义域为A，集合.
（Ⅰ）若，求；
（Ⅱ）若集合中恰有一个整数，求实数a的取值范围.

过曲线C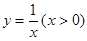：上一点作曲线C的切线，若切线的斜率为－4，则等于（   ）

A．2

B．

C．4

D．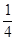

已知为不相等的两个正数，且，则函数和的图象之间的关系是（   ）

A．关于原点对称	B．关于y轴对称
C．关于x轴对称	D．关于直线对称

（本小题满分13分）盒中装有7个零件，其中5个是没有使用过的，2个是使用过的.
（Ⅰ）从盒中每次随机抽取1个零件，有放回的抽取3次，求3次抽取中恰有2次抽到使用过零件的概率；
（Ⅱ）从盒中任意抽取3个零件，使用后放回盒子中，设X为盒子中使用过零件的个数，求X的分布列和期望.

（本小题满分13分）在一次射击游戏中，规定每人最多射击3次；在A处击中目标得3分，在B，C处击中目标均得2分，没击中目标不得分；某同学在A处击中目标的概率为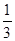，在B，C处击中目标的概率均为.
该同学依次在A，B，C处各射击一次，各次射击之间没有影响，求在一次游戏中：
（Ⅰ）该同学得4分的概率；
（Ⅱ）该同学得分少于5分的概率.

设，则＝____________；
_____________.

甲、乙两人分别从四种不同品牌的商品中选择两种，则甲、乙所选的商品中恰有一种品牌相同的选法种数是（   ）

A．30

B．24

C．12

D．6

（本大题满分10分）选修4-5：不等式选讲
设函数
（Ⅰ）解不等式；
（Ⅱ）当，时，证明：．

（本小题满分10分） 选修4-4：极坐标系与参数方程
在极坐标系中曲线的极坐标方程为，点．以极点为原点，以极轴为轴正半轴建立直角坐标系．斜率为的直线过点，且与曲线交于两点．
（Ⅰ）求出曲线的直角坐标方程和直线的参数方程；
（Ⅱ）求点到两点的距离之积．

设点P是函数图象上异于原点的动点，且该图象在点P处的切线的倾斜角为，则的取值范围是

A．

B．

C．

D．