已知
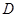 为
为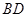 的中点,则
的中点,则 为( )
为( )

A.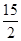 |
B.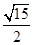 |
| C.7 | D.18 |
设有一个回归直线方程为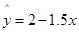 ,则变量
,则变量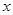 增加一个单位时( )
增加一个单位时( )
A.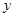 平均增加 1.5 个单位 平均增加 1.5 个单位 |
B.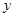 平均增加 2 个单位 平均增加 2 个单位 |
C.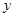 平均减少 1.5 个单位 平均减少 1.5 个单位 |
D.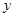 平均减少 2 个单位 平均减少 2 个单位 |
(本小题满分16分)已知数列 的前
的前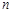 项和
项和 满足:
满足: ,数列
,数列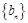 满足:对任意
满足:对任意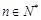 有
有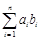
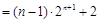 .
.
(1)求数列 与数列
与数列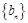 的通项公式;
的通项公式;
(2)记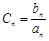 ,数列
,数列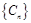 的前
的前 项和为
项和为 ,证明:当
,证明:当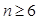 时,
时, .
.
(本小题满分14分)下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.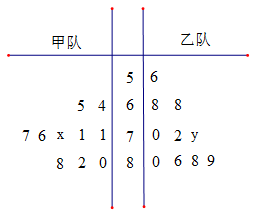
(1)求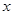 ,
,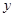 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
(本小题满分14分)已知数列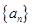 的前
的前 项和
项和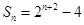 .
.
(1)求数列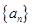 的通项公式;
的通项公式;
(2)设等差数列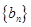 满足
满足 ,
,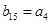 ,求数列
,求数列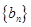 的前
的前 项和
项和 .
.
已知函数 的定义域为
的定义域为 ,若对任意
,若对任意 都有不等式
都有不等式 恒成立,则正实数m的取值范围是 .
恒成立,则正实数m的取值范围是 .
(本小题满分12分)已知向量 ,函数
,函数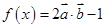
(1)求 的对称轴。
的对称轴。
(2)当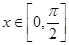 时,求
时,求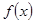 的最大值及对应的
的最大值及对应的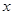 值。
值。
(本小题满分12分)已知向量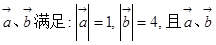 的夹角为
的夹角为 .
.
(1)求 ;(2)若
;(2)若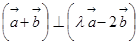 ,求
,求 的值.
的值.
(本小题满分12分)函数f(x)=3sin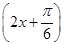 的部分图像如图所示.
的部分图像如图所示.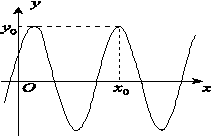
(1)写出f(x)的最小正周期及图中x0,y0的值;
(2)求f(x)在区间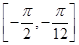 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(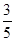 ,
,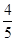 ),记∠COA=α.
),记∠COA=α.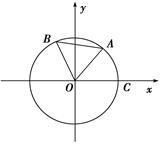
(Ⅰ)求 的值;
的值;
(Ⅱ)求cos∠COB的值.
函数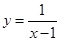 的图象与曲线
的图象与曲线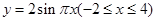 的所有交点的横坐标之和等于( )
的所有交点的横坐标之和等于( )
| A.2 | B.3 | C.4 | D.6 |
道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:
(Ⅰ)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(Ⅱ)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望,并指出所求期望的实际意义;
(Ⅲ)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.1和0.25,且每位驾驶员是否发生交通事故是相互独立的.依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率.(精确到0.01)并针对你的计算结果对驾驶员发出一句话的倡议.