(本小题满分10分)选修4-1:平面几何证明选讲
如图,在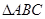 中,
中,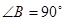 ,以
,以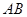 为直径的⊙
为直径的⊙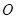 交
交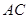 于
于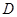 ,过点
,过点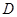 作⊙
作⊙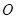 的切线交
的切线交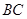 于
于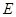 ,
,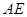 交⊙
交⊙ 于点
于点 .
.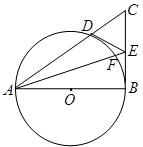
(Ⅰ)证明: 是
是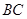 的中点;
的中点;
(Ⅱ)证明: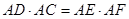 .
.
(本小题满分12分)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
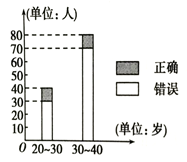
(Ⅰ) 完成2×2列联表;
 正误 正误年龄 |
正确 |
错误 |
合计 |
| 20~30 |
|
|
|
| 30~40 |
|
|
|
| 合计 |
|
|
|
(Ⅱ)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
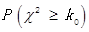 |
0.10 |
0.05 |
0.010 |
0.005 |
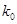 |
2.706 |
3.841 |
6.635 |
7.879 |
(参考公式: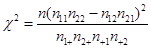 ,
,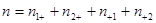 )
)
给出下列四个命题:
①使用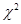 统计量作
统计量作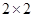 列联表的独立性检验时,要求表中的4个数据都要大于10;
列联表的独立性检验时,要求表中的4个数据都要大于10;
②使用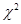 统计量进行独立性检验时,若
统计量进行独立性检验时,若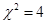 ,则有
,则有 的把握认为两个事件有关;
的把握认为两个事件有关;
③回归直线就是散点图中经过样本数据点最多的那条直线
④在线性回归分析中,如果两个变量的相关性越强,则相关系数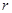 就越接近于1.
就越接近于1.
其中真命题的个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
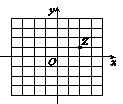
若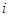 为虚数单位,图中网格纸的小正方形的边长是1,复平面内点
为虚数单位,图中网格纸的小正方形的边长是1,复平面内点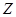 表示复数
表示复数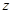 ,则复数
,则复数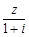 对应的点位于复平面内的( )
对应的点位于复平面内的( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
(本小题共14分)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为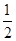 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为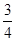 ,
,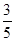 .
.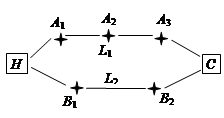
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数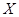 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
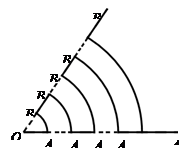
如图所示,∠AOB=1rad,点Al,A2,…在OA上,点B1,B2,…在OB上,其中的每一个实线段和虚线段的长均为1个长度单位,一个动点M从O点出发,沿着实线段和以O为圆心的圆弧匀速运动,速度为l长度单位/秒,则质点M到达A3点处所需要的时间为 秒,质点M到达An点处所需要的时间为 秒.