(本小题满分14分)已知三棱锥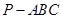 中,
中,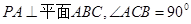 ,
,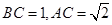 .如图,从由任何二个顶点确定的向量中任取两个向量,记变量
.如图,从由任何二个顶点确定的向量中任取两个向量,记变量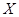 为所取两个向量的数量积的绝对值.
为所取两个向量的数量积的绝对值.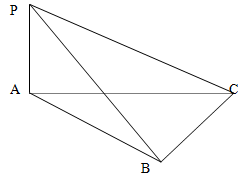
(1)当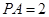 时,求
时,求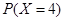 的值.
的值.
(2)当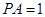 时,求变量
时,求变量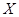 的分布列与期望.
的分布列与期望.
(本小题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段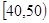 ,
,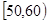 …
…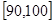 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: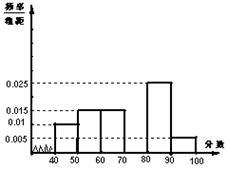
(1)求第四小组的频率,补全这个频率分布直方图;并估计该校学生的数学成绩的中位数.
(2)从数学成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
(3)若从全市参加高一年级期末考试的学生中,任意抽取4个学生,设这四个学生中数学成绩为80分以上(包括80分)的人数为X,(以该校学生的成绩的频率估计概率),求X的数学期望.
(本小题满分12分)
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得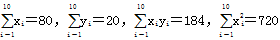 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,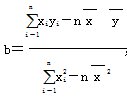 ,a=
,a= -b
-b 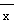 ,其中
,其中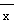 ,
, 为样本平均值.
为样本平均值.
一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c ∈(0,1)),已知他投篮一次得分的数学期望为2(不计其他得分情况),则ab的最大值为( )
A.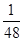 |
B.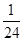 |
C.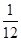 |
D.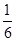 |
(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点,极轴与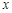 轴的正半轴重合,直线
轴的正半轴重合,直线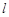 的参数方程为
的参数方程为
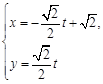 (
(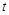 为参数),圆
为参数),圆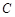 的极坐标方程为
的极坐标方程为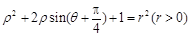 .
.
(1)求直线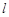 的普通方程和圆
的普通方程和圆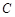 的直角坐标方程;
的直角坐标方程;
(2)若圆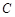 上的点到直线
上的点到直线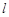 的最大距离为
的最大距离为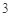 ,求
,求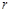 的值.
的值.
(本小题满分12分)已知函数
(Ⅰ)若函数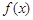 在
在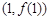 处的切线垂直于
处的切线垂直于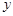 轴,求实数a的值;
轴,求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,求函数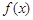 的单调区间;
的单调区间;
(Ⅲ)若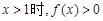 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
(共12分)已知方程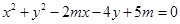 的曲线是圆C
的曲线是圆C
(1)求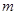 的取值范围;
的取值范围;
(2)当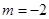 时,求圆C截直线
时,求圆C截直线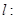
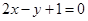 所得弦长;
所得弦长;
(本小题共12分)长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).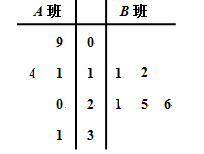
(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过21的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.