如图1,在直角梯形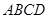 中,
中, ,
,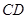 ∥
∥ ,
,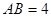 ,
,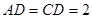 ,将
,将 沿
沿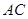 折起,使平面
折起,使平面 平面
平面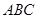 ,得到几何体
,得到几何体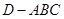 ,如图2所示.
,如图2所示.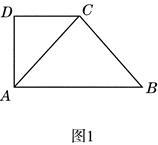
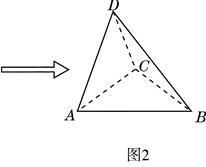
(1)求证: 平面
平面 ;
;
(2)求几何体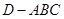 的体积.
的体积.
(本小题满分12分)已知向量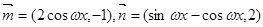
 ,
,
函数 ,若函数
,若函数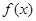 的图象的两个相邻对称中心的距离为
的图象的两个相邻对称中心的距离为 .
.
(Ⅰ)求函数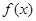 的单调增区间;
的单调增区间;
(Ⅱ)若将函数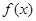 的图象先向左平移
的图象先向左平移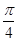 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的 倍,得到函数
倍,得到函数 的图象,当
的图象,当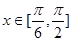 时,求函数
时,求函数 的值域.
的值域.
周期为4的奇函数 在
在 上的解析式为
上的解析式为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知x、 y满足约束条件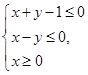 则 z =" x" + 2y 的最大值为
则 z =" x" + 2y 的最大值为
| A.-2 | B.-1 | C.1 | D.2 |
如图,下列四个几何题中,它们的三视图(主视图、俯视图、侧视图)有且仅有两个相同,而另一个不同的两个几何体是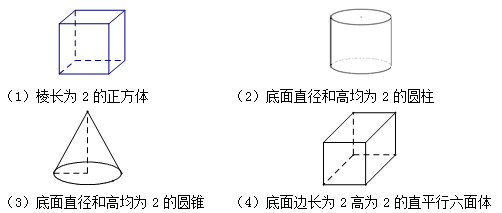
| A.(1)、(2) | B.(1)、(3) | C.(2)、(3) | D.(1)、(4) |
设α为锐角,若cos =
= ,则sin
,则sin 的值为( )
的值为( )
A. |
B.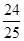 |
C. |
D. |
极坐标系的极点在直角坐标系的原点,极轴与 轴的正半轴重合,直线
轴的正半轴重合,直线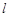 的参数方程为
的参数方程为
 (
( 为参数), 圆
为参数), 圆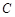 的极坐标方程为
的极坐标方程为 .
.
(1)求直线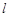 的普通方程和圆
的普通方程和圆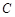 的直角坐标方程;
的直角坐标方程;
(2)若圆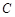 上的点到直线
上的点到直线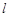 的最大距离为
的最大距离为 ,求
,求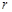 的值.
的值.
如图,在直三棱柱 中,
中,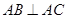 ,
, ,
,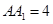 ,点
,点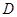 是
是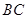 的中点.
的中点.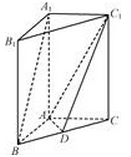
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)求平面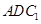 与平面
与平面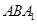 所成二面角的正弦值.
所成二面角的正弦值.
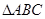 的三个内角
的三个内角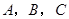 对应的三条边长分别是
对应的三条边长分别是 ,且满足
,且满足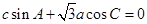
(1)求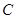 的值;
的值;
(2)若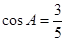 ,
,  ,求
,求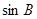 和
和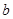 的值.
的值.
已知函数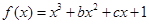 有两个极值点
有两个极值点 且
且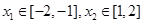 ,则
,则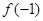 的取值范围是( )
的取值范围是( )
A.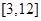 |
B.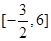 |
C. |
D. |
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
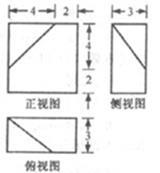
| A.108cm3 | B.100 cm3 | C.92cm3 | D.84cm3 |
某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,得到成绩分布的频率分布直方图如图:
(1)若规定60分以上为合格,计算高一年级这次知识竞赛的合格率;
(2)将上述调查所得到的频率视为概率.现在从该校大量高一学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的合格人数为X.若每次抽取的结果是相互独立的,求X的分布列和期望E(X);
(3)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写2×2列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”.

一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数ξ的分布列为:
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元. 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求η的分布列及期望E( ).
).