已知定义在 上的偶函数满足:
上的偶函数满足: ,且当
,且当 时,
时, 单调递减,给出以下四个命题:
单调递减,给出以下四个命题:
① ;
;
② 为函数
为函数 图象的一条对称轴;
图象的一条对称轴;
③  在
在 单调递增;
单调递增;
④若方程 在
在 上的两根为
上的两根为 、
、 ,则
,则
以上命题中所有正确命题的序号为___________.
已知抛物线 上一定点B(1,1)和两个动点P、Q,当P在抛物线上运动时,BP⊥PQ,则Q点的纵坐标的取值范围是( )
上一定点B(1,1)和两个动点P、Q,当P在抛物线上运动时,BP⊥PQ,则Q点的纵坐标的取值范围是( )
A. |
B. |
C. |
D. |
一个空间几何体的三视图如下图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为( )

A. |
B. |
C. |
D. |
选修4—4:坐标系与参数方程
直线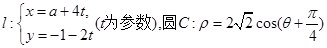 (极轴与
(极轴与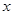 轴的非负半轴重合,且单位长度相同)。
轴的非负半轴重合,且单位长度相同)。
(1)求圆心C到直线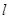 的距离;
的距离;
(2)若直线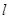 被圆C截的弦长为
被圆C截的弦长为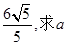 的值。
的值。
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形 是⊙
是⊙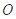 的内接四边形,延长
的内接四边形,延长 和
和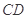 相交于点
相交于点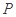 ,
,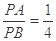 ,
,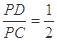 .
.
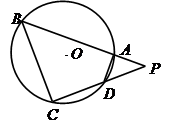
(Ⅰ)求 的值;
的值;
(Ⅱ)若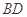 为⊙
为⊙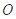 的直径,且
的直径,且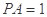 ,求
,求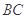 的长.
的长.
(本小题满分12分)甲、乙、丙三人射击同一目标,各射击一次,已知甲击中目标的概率为 ,乙与丙击中目标的概率分别为
,乙与丙击中目标的概率分别为
 ,每人是否击中目标是相互独立的.记目标被击中的次数为
,每人是否击中目标是相互独立的.记目标被击中的次数为 ,且
,且 的分布列如下表:
的分布列如下表:
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的数学期望.
的数学期望.
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,左视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )

A. |
B.4 |
C. |
D. |
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系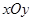 中,直线
中,直线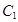 的参数方程为
的参数方程为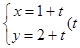 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点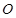 为极点,
为极点,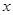 轴的非负半轴为极轴的极坐标系下,圆
轴的非负半轴为极轴的极坐标系下,圆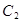 的方程为
的方程为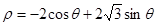 .
.
(Ⅰ)求直线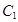 的普通方程和圆
的普通方程和圆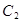 的圆心的极坐标;
的圆心的极坐标;
(Ⅱ)设直线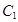 和圆
和圆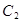 的交点为
的交点为 、
、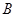 ,求弦
,求弦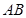 的长.
的长.