双曲线 (a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是
(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是
A.(1, ] ] |
B.(1, ) ) |
C.(1,2 ] ] |
D.(1,2 ) ) |
(本题10分)
在平面直角坐标系 中,已知直线
中,已知直线 :
: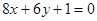 ,圆
,圆 ,圆
,圆 .
.
(1)当 时,试判断圆
时,试判断圆 与圆
与圆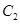 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若圆 与圆
与圆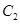 关于直线
关于直线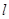 对称,求
对称,求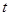 的值;
的值;
(3)在(2)的条件下,若 为平面上的点,是否存在过点
为平面上的点,是否存在过点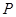 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线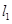 和
和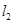 ,它们分别与圆
,它们分别与圆 和
和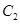 相交,且直线
相交,且直线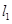 被圆
被圆 截得的弦长与直线
截得的弦长与直线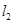 被圆
被圆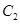 截得的弦长相等,若存在,求点
截得的弦长相等,若存在,求点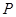 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题14分) 已知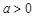 且
且 ,函数
,函数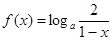 .
.
(1)求 的定义域
的定义域 及其零点;
及其零点;
(2)讨论并用函数单调性定义证明函数 在定义域
在定义域 上的单调性;
上的单调性;
(3)设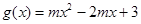 ,当
,当 时,若对任意
时,若对任意 ,存在
,存在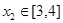 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题12分) 已知函数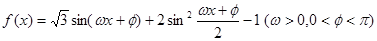 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为 .
.
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)将函数 的图象沿
的图象沿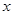 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的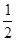 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当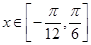 时,求函数
时,求函数 的值域.
的值域.
(本小题12分) 已知定圆
 ,定直线
,定直线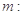
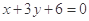 ,过
,过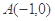 的一条动直线
的一条动直线 与直线相交于
与直线相交于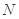 ,与圆
,与圆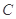 相交于
相交于 两点,
两点,
(1)当 与
与 垂直时,求出
垂直时,求出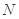 点的坐标,并证明:
点的坐标,并证明: 过圆心
过圆心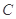 ;
;
(2)当 时,求直线
时,求直线 的方程.
的方程.
某产品的广告费用 与销售额
与销售额 的统计数据如下表:
的统计数据如下表:
广告费用 (万元) (万元) |
4 |
2 |
3 |
5 |
销售额 (万元) (万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程 中的
中的 为
为 ,据此模型预报广告费用为6万元时销售额为( )
,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
.设有关于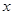 的一元二次方程
的一元二次方程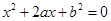 .
.
(Ⅰ)若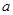 是从
是从 四个数中任取的一个数,
四个数中任取的一个数,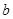 是从
是从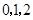 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若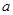 是从区间
是从区间 任取的一个数,
任取的一个数,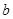 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.