如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为 ,则
,则 的最大值为 .
的最大值为 .

如图, 是双曲线的左、右焦点,过
是双曲线的左、右焦点,过 的直线
的直线 与双曲线的左右两支分别交于点
与双曲线的左右两支分别交于点 、
、 两点,若
两点,若 为等边三角形,则该双曲线的离心率为 .
为等边三角形,则该双曲线的离心率为 .

定义区间 的长度为
的长度为
 ,函数
,函数 的定义域与值域都是
的定义域与值域都是 ,则区间
,则区间 取最大长度时实数
取最大长度时实数 的值为( )
的值为( )
A. |
B.-3 | C.1 | D.3 |
设集合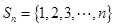 ,若Z是
,若Z是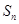 的子集,把Z中的所有数的和称为Z的“容量”(规定空集的容量为0).若Z的容量为奇(偶)数,则称Z为
的子集,把Z中的所有数的和称为Z的“容量”(规定空集的容量为0).若Z的容量为奇(偶)数,则称Z为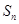 的奇(偶)子集.
的奇(偶)子集.
命题①: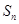 的奇子集与偶子集个数相等;
的奇子集与偶子集个数相等;
命题②:当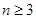 时,
时,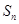 的所有奇子集的容量之和与所有偶子集的容量之和相等
的所有奇子集的容量之和与所有偶子集的容量之和相等
则下列说法正确的是( )
| A.命题①和命题②都成立 |
| B.命题①和命题②都不成立 |
| C.命题①成立,命题②不成立 |
| D.命题①不成立,命题②成立 |
“直线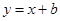 与圆
与圆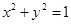 相交”是“
相交”是“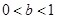 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
(本小题满分12分)
已知函数 =ax3—
=ax3— (1+a)x2 +3x -3(其中a∈R)
(1+a)x2 +3x -3(其中a∈R)
(I)若函数 在x= -1时取得极值,求a;
在x= -1时取得极值,求a;
(Ⅱ)求函数 的单调区间.
的单调区间.
(本小题满分12分)
设命题p:实数x满足|x-1|≤m,,其中m>0,命题q:-2<x≤10
(I)若m=2且p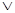 q为真命题,求实数x的取值范围;
q为真命题,求实数x的取值范围;
(Ⅱ)若 q是
q是 P的充分不必要条件,求实数m的取值范围.
P的充分不必要条件,求实数m的取值范围.
设[x]表示不大于x的最大整数,函数 =[x]-x,则f(f(1.5))= ( )
=[x]-x,则f(f(1.5))= ( )
| A.一l | B.— |
C. |
D.1 |
已知函数 =|x-1|,则下列函数中与
=|x-1|,则下列函数中与 相同的函数是( )
相同的函数是( )
A.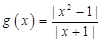 |
B. |
C. |
D.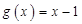 |
(本小题满分12分)
已知函数 = 21nx—x2+ax(a
= 21nx—x2+ax(a R)
R)
(I)当a=2时,求 的图象在x=l处的切线方程;
的图象在x=l处的切线方程;
(Ⅱ)若函数 的图象与x轴有两个不同的交点A(x1,0),B( x2,0)(0< x1< x2),
的图象与x轴有两个不同的交点A(x1,0),B( x2,0)(0< x1< x2),
求证: (其中
(其中 为
为 的导函数)
的导函数)
(本小题满分12分)
已知函数
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)若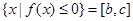 (其中b<c),求a的取值范围,并说明[b,c]
(其中b<c),求a的取值范围,并说明[b,c] (0,1)。
(0,1)。