已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若曲线C1的方程为ρ2=8ρsinθ﹣15,曲线 C2的方程为 (
( 为参数).
为参数).
(1)将C1的方程化为直角坐标方程;
(2)若C2上的点Q对应的参数为 ,P为C1上的动点,求PQ的最小值.
,P为C1上的动点,求PQ的最小值.
如图所示,AB是半径为1的圆O的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.
(1)求证:AE•BC=AC•BD;
(2)求BC•BE+AC•AD的值.
已知函数f(x)=1﹣ax+lnx,
(1)若函数在x=2处的切线斜率为 ,求实数a的值;
,求实数a的值;
(2)若存在x∈(0,+∞)使f(x)≥0成立,求实数a的范围;
(3)证明对于任意n∈N,n≥2有: .
.
设定义在R上的函数f(x)对于任意x,y都有f(x+y)=f(x)+f(y)成立,且f(1)=﹣2,当x>0时,f(x)<0.
(1)判断f(x)在R上的单调性,并加以证明;
(2)当﹣2015≤x≤2015时,不等式f(x)≤k恒成立,求实数k的取值范围.
定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
| A.{x|x>0} | B.{x|x<0} |
| C.{x|x<﹣1或x>1} | D.{x|x<﹣1或0<x<1} |
设某中学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
| A.y与x具有正的线性相关关系 |
| B.回归直线至少经过样本数据(xi,yi)(i=1,2,…,n)中的一个 |
| C.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
D.回归直线一定过样本点的中心点 |
已知函数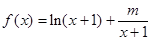 .
.
(1)当函数 在点
在点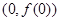 处的切线与直线
处的切线与直线 垂直时,求实数
垂直时,求实数 的值;
的值;
(2)若 时,
时,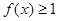 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知书架中甲层有英语书2本和数学书3本,乙层有英语书1本和数学书4本.现从甲、乙两层中各取两本书.
(1)求取出的4本书都是数学书的概率.
(2)求取出的4本书中恰好有1本是英语书的概率.