2022年中考数学专题:锐角三角函数(一)
如图,在建筑物 左侧距楼底 点水平距离150米的 处有一山坡,斜坡 的坡度(或坡比)为 ,坡顶 到 的垂直距离 米(点 , , , , 在同一平面内),在点 处测得建筑物顶 点的仰角为 ,则建筑物 的高度约为
(参考数据: ; ;

| A. |
69.2米 |
B. |
73.1米 |
C. |
80.0米 |
D. |
85.7米 |
如图,四边形 是菱形,对角线 , 相交于点 , , ,点 是 上一动点,点 是 的中点,则 的最小值为

| A. |
|
B. |
|
C. |
3 |
D. |
|
如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在正方形 中,对角线 与 相交于点 ,点 在 的延长线上,连接 ,点 是 的中点,连接 交 于点 ,连接 ,若 , .则下列结论:① ;② ;③ ;④ ;⑤点 到 的距离为 .其中正确的结论是
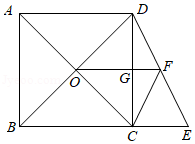
| A. |
①②③④ |
B. |
①③④⑤ |
C. |
①②③⑤ |
D. |
①②④⑤ |
如图,相邻两个山坡上,分别有垂直于水平面的通信基站 和 .甲在山脚点 处测得通信基站顶端 的仰角为 ,测得点 距离通信基站 的水平距离 为 ;乙在另一座山脚点 处测得点 距离通信基站 的水平距离 为 ,测得山坡 的坡度 .若 ,点 , , , 在同一水平线上,则两个通信基站顶端 与顶端 的高度差为(参考数据: ,

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯 的坡度 为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端 以0.5米 秒的速度用时40秒到达扶梯顶端 ,则王老师上升的铅直高度 为 米.

由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中 的长应是 .

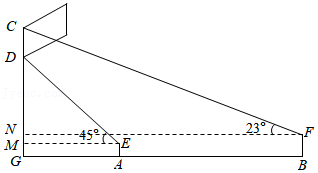
某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头 测一段水平雪道一端 处的俯角为 ,另一端 处的俯角为 ,若无人机镜头 处的高度 为238米,点 , , 在同一直线上,则雪道 的长度为 米.(结果保留整数,参考数据 , ,

如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点.若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .

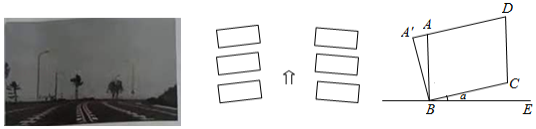
高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形 表示一个"鱼骨", 平行于车辆前行方向, , ,过 作 的垂线,垂足为 点的视觉错觉点),若 , ,则 .
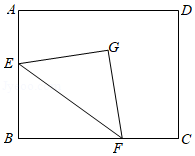
如图,在矩形 中, , ,点 , 分别是边 , 上的动点,点 不与 , 重合,且 , 是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点 到边 , 的距离一定相等;
③点 到边 , 的距离可能相等;
④点 到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
如图,一艘货船在灯塔 的正南方向,距离灯塔257海里的 处遇险,发出求救信号.一艘救生船位于灯塔 的南偏东 方向上,同时位于 处的北偏东 方向上的 处,救生船接到求救信号后,立即前往救援.求 的长(结果取整数)参考数据: , 取1.73.

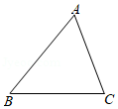
如图,已知锐角 中, .

(1)请在图1中用无刻度的直尺和圆规作图:作 的平分线 ;作 的外接圆 ;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若 , 的半径为5,则 .(如需画草图,请使用图
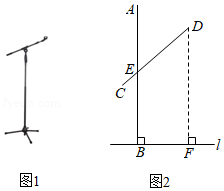
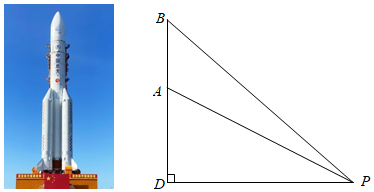
图1是放置在水平地面上的落地式话筒架实物图,图2是其示意图.支撑杆 垂直于地面 ,活动杆 固定在支撑杆上的点 处.若 , , ,求活动杆端点 离地面的高度 .(结果精确到 ,参考数据: , ,
问题提出
(1)如图1,在 中, , , , 是 的中点,点 在 上,且 ,求四边形 的面积.(结果保留根号)
问题解决
(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上规划一个五边形河畔公园 .按设计要求,要在五边形河畔公园 内挖一个四边形人工湖 ,使点 、 、 、 分别在边 、 、 、 上,且满足 , .已知五边形 中, , , , , .为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形 面积的最小值及这时点 到点 的距离;若不存在,请说明理由.
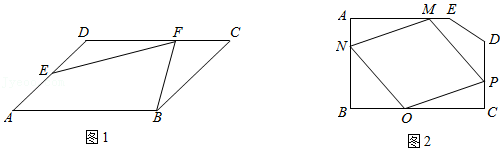
已知,在 中, , .

(1)如图1,已知点 在 边上, , ,连结 .试探究 与 的关系;
(2)如图2,已知点 在 下方, , ,连结 .若 , , , 交 于点 ,求 的长;
(3)如图3,已知点 在 下方,连结 、 、 .若 , , , ,求 的值.
今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在 处测得国旗 处的仰角为 ,站在同一队列 处的小刚测得国旗 处的仰角为 ,已知小明目高 米,距旗杆 的距离为15.8米,小刚目高 米,距小明24.2米,求国旗的宽度 是多少米?(最后结果保留一位小数)
(参考数据: , ,
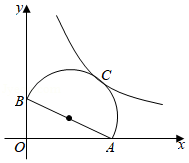
如图, 内接于 , 是 的直径 的延长线上一点, .过圆心 作 的平行线交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的值.

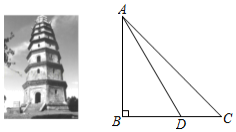
全国历史文化名城宜宾有许多名胜古迹,始建于明朝的白塔是其中之一.如图,为了测量白塔的高度 ,在 处测得塔顶 的仰角为 ,再向白塔方向前进15米到达 处,又测得塔顶 的仰角为 ,点 、 、 在同一水平线上,求白塔的高度 . ,精确到1米)
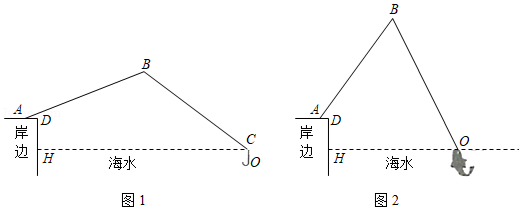
我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端 离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点 到岸边 的距离;
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点 恰好位于海面.求点 到岸边 的距离.
(参考数据: , , , , ,





 粤公网安备 44130202000953号
粤公网安备 44130202000953号