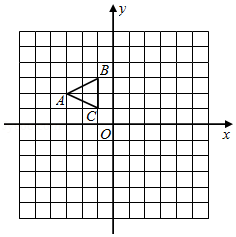
已知: 三个顶点的坐标分别为 , , .
(1)画出 关于 轴对称的△ ;
(2)以点 为位似中心,将 放大为原来的2倍,得到△ ,请在网格中画出△ ,并写出点 的坐标.

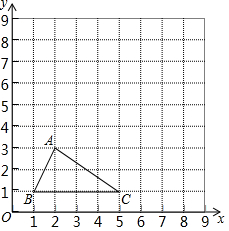
在平面直角坐标系中, 三个顶点的坐标分别为 , , .
(1)把 平移后,其中点 移到点 ,画出平移后得到的△ ;
(2)把△ 绕点 按逆时针方向旋转 ,画出旋转后的△ .
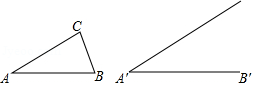
求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的 及线段 , ,以线段 为一边,在给出的图形上用尺规作出△ ,使得△ ,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
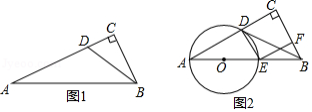
如图1, 中, ,点 在 上, ,过 、 两点的圆的圆心 在 上.
(1)利用直尺和圆规在图1中画出 (不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断 所在直线与(1)中所作的 的位置关系,并证明你的结论;
(3)设 交 于点 ,连接 ,过点 作 , 为垂足,若点 是线段 的黄金分割点(即 ,如图2,试说明四边形 是正方形).
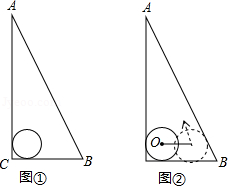
如图, 是一块直角三角板,且 , ,现将圆心为点 的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边 、 都相切时,试用直尺与圆规作出射线 ;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若 ,圆形纸片的半径为2,求圆心 运动的路径长.
如图,已知等边 ,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹)
(1)作 的外心 ;
(2)设 是 边上一点,在图中作出一个正六边形 ,使点 ,点 分别在边 和 上.
如图,已知 ,及线段 , .
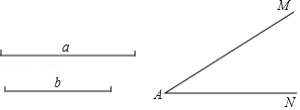
(1)仅用没有刻度的直尺和圆规分别在射线 、 上确定点 、点 ,使得 , (保留作图痕迹,不要作法);
(2)若 , , ,则 的面积为 .
如图,已知 ,及线段 , .

(1)仅用没有刻度的直尺和圆规分别在射线 、 上确定点 、点 ,使得 , (保留作图痕迹,不要作法);
(2)若 , , ,则 的面积为 .
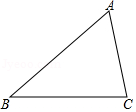
如图, 中, .
(1)用直尺和圆规在 的内部作射线 ,使 (不要求写作法,保留作图痕迹);
(2)若(1)中的射线 交 于点 , , ,求 的长.
“直角”在初中几何学习中无处不在.
如图,已知 ,请仿照小丽的方式,再用两种不同的方法判断 是否为直角(仅限用直尺和圆规).

如图,已知△ABC,请用圆规和直尺作出△ABC的一条中位线EF(不写作法,保留作图痕迹).
在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).
(1)以(0,0)为圆心,3为半径画圆;
(2)以(0,﹣1)为圆心,1为半径向下画半圆;
(3)分别以(﹣1,1),(1,1)为圆心,0.5为半径画圆;
(4)分别以(﹣1,1),(1,1)为圆心,1为半径向上画半圆.
(向上、向下指在经过圆心的水平线的上方和下方)
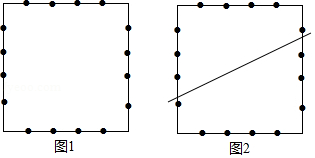
小琪同学和爸爸妈妈一起回老家给奶奶过生日,他们为奶奶准备了一个如图所示的正方形蛋糕,蛋糕的每条边上均匀镶嵌着4颗巧克力.爸爸要求小琪只切两刀把蛋糕平均分成4份,使每个人分得的蛋糕和巧克力数都相等.
(1)请你在图1中画出一种分法(无需尺规作图);
(2)如图2,小琪同学过正方形的中心切了一刀,请你用尺规作图帮她作出第2刀所在的直线.(不写作法,保留作图痕迹)
如图所示的平面直角坐标系中, 的三个顶点坐标分别为 , , ,请按如下要求画图:
(1)以坐标原点 为旋转中心,将 顺时针旋转 ,得到△ ,请画出△ ;
(2)以坐标原点 为位似中心,在 轴下方,画出 的位似图形△ ,使它与 的位似比为 .