初中数学解答题

受疫情影响，某初中学校进行在线教学的同时，要求学生积极参与“增强免疫力、丰富学习生活”为主题的居家体育锻炼活动，并实施锻炼时间目标管理．为确定一个合理的学生居家锻炼时间的完成目标，学校随机抽取了30名学生周累计居家锻炼时间（单位：h）的数据作为一个样本，并对这些数据进行了收集、整理和分析，过程如下：

【数据收集】

7 8 6 5 9 10 4 6 7 5 11 12 8 7 6

4 6 3 6 8 9 10 10 13 6 7 8 3 5 10

【数据整理】

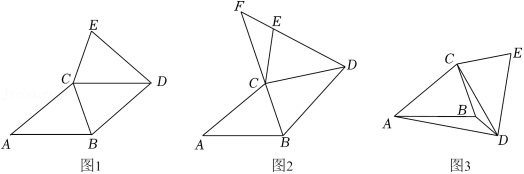
将收集的30个数据按A，B，C，D，E五组进行整理统计，并绘制了如图所示的不完整的频数分布直方图（说明： $A.3\le t＜5,B.5\le t＜7,C.7\le t＜9,D.9\le t＜11,E.11\le t\le 13$，其中t表示锻炼时间）；

【数据分析】

统计量	平均数	众数	中位数
锻炼时间（h）	7.3	m	7

请根据以上信息解答下列问题：

（1）填空：m＝　 　；

（2）补全频数分布直方图；

（3）如果学校将管理目标确定为每周不少于7h，该校有600名学生，那么估计有多少名学生能完成目标？你认为这个目标合理吗？说明理由．

第24届冬季奥林匹克运动会于2022年2月4至20日在我国北京﹣张家口成功举办，其中张家口赛区设有四个冬奥会竞赛场馆，分别为：A．云顶滑雪公园、B．国家跳台滑雪中心、C．国家越野滑雪中心、D．国家冬季两项中心．小明和小颖都是志愿者，他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同．

（1）小明被分配到D．国家冬季两项中心场馆做志愿者的概率是多少？

（2）利用画树状图或列表的方法，求小明和小颖被分配到同一场馆做志愿者的概率．

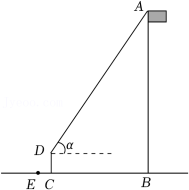
灞陵桥位于甘肃省渭源县城南清源河（渭河上游）上，始建于明洪武初年，因“渭水绕长安，绕灞陵，为玉石栏杆灞陵桥”之语，得名灞陵桥（图1），该桥为全国独一无二的纯木质叠梁拱桥．某综合实践研究小组开展了测量汛期某天“灞陵桥拱梁顶部到水面的距离”的实践活动，过程如下：

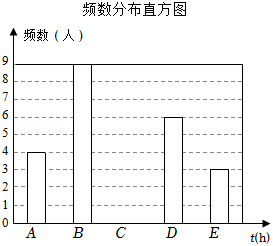
方案设计：如图2，点C为桥拱梁顶部（最高点），在地面上选取A，B两处分别测得∠CAF和∠CBF的度数（A，B，D，F在同一条直线上），河边D处测得地面AD到水面EG的距离DE（C，F，G在同一条直线上， $DF\parallel EG,CG\perp AF,FG＝DE$）．

数据收集：实地测量地面上A，B两点的距离为8.8m，地面到水面的距离 $DE＝1.5m,\angle CAF＝26.6°,\angle CBF＝35°$．

问题解决：求灞陵桥拱梁顶部C到水面的距离CG（结果保留一位小数）．

参考数据： $\sin 26.6°\approx 0.45,\cos 26.6°\approx 0.89,\tan 26.6°\approx 0.50,\sin 35°\approx 0.57,\cos 35°\approx 0.82,\tan 35°\approx 0.70$．

根据上述方案及数据，请你完成求解过程．

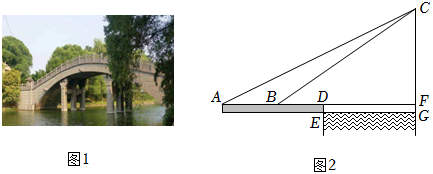
中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编（图1），书中记载了大量几何作图题，所有内容均用浅近的文言文表述，第一编记载了这样一道几何作图题：

原文	释义
甲乙丙为定直角． 以乙为圆心，以任何半径作丁戊弧； 以丁为圆心，以乙丁为半径画弧得交点己； 再以戊为圆心，仍以原半径画弧得交点庚； 乙与己及庚相连作线．	如图2，∠ABC为直角， 以点B为圆心，以任意长为半径画弧，交射线BA，BC分别于点D，E； 以点D为圆心，以BD长为半径画弧与 $\stackrel{̂}{\mathit{DE}}$交于点F； 再以点E为圆心，仍以BD长为半径画弧与 $\stackrel{̂}{\mathit{DE}}$交于点G； 作射线BF，BG．

（1）根据以上信息，请你用不带刻度的直尺和圆规，在图2中完成这道作图题（保留作图痕迹，不写作法）；

（2）根据（1）完成的图，直接写出 $\angle DBG,\angle GBF,\angle FBE$的大小关系．

如图，在菱形 $ABCD$中， $\angle BAD＝120°$， $AB＝6$，连接 $BD$．

（1）求 $BD$的长；

（2）点E为线段 $BD$上一动点（不与点B，D重合），点 $F$在边 $AD$上，且 $BE=\sqrt{3}DF$．

①当 $CE\perp AB$时，求四边形 $ABEF$的面积；

②当四边形 $ABEF$的面积取得最小值时， $CE+\sqrt{3}CF$的值是否也最小？如果是，求 $CE+\sqrt{3}CF$的最小值；如果不是，请说明理由．

已知直线 $l：y＝kx+b$经过点 $（0,7）$和点 $（1,6）$．

（1）求直线 $l$的解析式；

（2）若点 $P（m,n）$在直线l上，以P为顶点的抛物线G过点 $（0,﹣3）$，且开口向下．

①求m的取值范围；

②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点 $Q\prime$也在G上时，求G在 $\frac{4m}{5}\le x\le \frac{4m}{5}+1$的图象的最高点的坐标．

某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE， $CD＝1.6m,BC＝5CD$．

（1）求 $BC$的长；

（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．

条件①： $CE＝1.0m$；条件②：从D处看旗杆顶部A的仰角 $\alpha$为 $54.46°$．

注：如果选择条件①和条件②分别作答，按第一个解答计分．

参考数据： $\sin 54.46°\approx 0.81,\cos 54.46°\approx 0.58,\tan 54.46°\approx 1.40$．

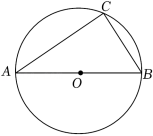
如图，AB是⊙O的直径，点C在⊙O上，且 $AC＝8,BC＝6$．

（1）尺规作图：过点O作AC的垂线，交劣弧 $\stackrel{̂}{\mathit{AC}}$于点D，连接CD（保留作图痕迹，不写作法）；

（2）在（1）所作的图形中，求点O到AC的距离及 $\sin \angle ACD$的值．

已知 $T=（a+3b{）}^2+（2a+3b）（2a﹣3b）+a^2$．

（1）化简 $T$；

（2）若关于 $x$的方程 $x^2+2ax﹣ab+1＝0$有两个相等的实数根，求 $T$的值．

某燃气公司计划在地下修建一个容积为 $V$（ $V$为定值，单位： $m^3$）的圆柱形天然气储存室，储存室的底面积 $S$（单位： $m^2$）与其深度 $d$（单位： $m$）是反比例函数关系，它的图象如图所示．

（1）求储存室的容积V的值；

（2）受地形条件限制，储存室的深度d需要满足 $16\le d\le 25$，求储存室的底面积S的取值范围．

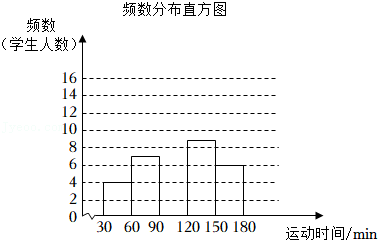
某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．

频数分布表

运动时间t/min	频数	频率
$30\le t＜60$	4	0.1
$60\le t＜90$	7	0.175
$90\le t＜120$	a	0.35
$120\le t＜150$	9	0.225
$150\le t＜180$	6	b
合计	n	1

请根据图表中的信息解答下列问题：

（1）频数分布表中的a＝　 　，b＝　 　，n＝　 　；

（2）请补全频数分布直方图；

（3）若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数．

如图，点D，E在△ABC的边BC上， $\angle B＝\angle C,BD＝CE$，求证： $△ABD≌△ACE$．

在平面直角坐标系 $xOy$中，已知抛物线 $y＝a{x}^2+bx$经过 $A（4,0）,B（1,4）$两点． $P$是抛物线上一点，且在直线 $AB$的上方．

（1）求抛物线的解析式；

（2）若 $△OAB$面积是 $△PAB$面积的2倍，求点 $P$的坐标；

（3）如图， $OP$交 $AB$于点 $C$， $PD\parallel BO$交 $AB$于点 $D$．记 $△CDP$， $△CPB$, $△CBO$的面积分别为 $S_1,S_2,S_3$．判断 $\frac{S_1}{S_2}+\frac{S_2}{S_3}$是否存在最大值．若存在，求出最大值；若不存在，请说明理由．

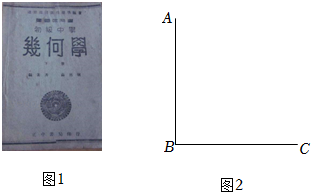
已知 $△ABC≌△DEC$， $AB＝AC$， $AB＞BC$．

（1）如图1， $CB$平分 $\angle ACD$，求证：四边形 $ABDC$是菱形；

（2）如图2，将（1）中的 $△CDE$绕点 $C$逆时针旋转（旋转角小于 $\angle BAC$）， $BC,DE$的延长线相交于点 $F$，用等式表示 $\angle ACE$与 $\angle EFC$之间的数量关系，并证明；

（3）如图3，将（1）中的 $△CDE$绕点 $C$顺时针旋转（旋转角小于 $\angle ABC$），若 $\angle BAD＝\angle BCD$，求 $\angle ADB$的度数．

如图，BD是矩形ABCD的对角线．

（1）求作 $\odot A$，使得 $\odot A$与 $BD$相切（要求：尺规作图，不写作法，保留作图痕迹）；

（2）在（1）的条件下，设BD与 $\odot A$相切于点E， $CF\perp BD$，垂足为F．若直线CF与 $\odot A$相切于点G，求 $\tan \angle ADB$的值．