为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到图表:
该地区每周接种疫苗人数统计表
周次 |
第1周 |
第2周 |
第3周 |
第4周 |
第5周 |
第6周 |
第7周 |
第8周 |
接种人数(万人) |
7 |
10 |
12 |
18 |
25 |
29 |
37 |
42 |

根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3周开始这些点大致分布在一条直线附近,现过其中两点 、 作一条直线(如图所示,该直线的函数表达式为 ,那么这条直线可近似反映该地区接种人数的变化趋势.
请根据以上信息,解答下列问题:
(1)这八周中每周接种人数的平均数为 万人;该地区的总人口约为 万人;
(2)若从第9周开始,每周的接种人数仍符合上述变化趋势.
①估计第9周的接种人数约为 万人;
②专家表示:疫苗接种率至少达 ,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
(3)实际上,受疫苗供应等客观因素,从第9周开始接种人数将会逐周减少 万人,为了尽快提高接种率,一旦周接种人数低于20万人时,卫生防疫部门将会采取措施,使得之后每周的接种能力一直维持在20万人.如果 ,那么该地区的建议接种人群最早将于第几周全部完成接种?

某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;
(2)在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图 ,此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , ,

在平面直角坐标系中, 为坐标原点,直线 与 轴交于点 ,与 轴交于点 ,二次函数 的图象过 、 两点,且与 轴交于另一点 ,点 为线段 上的一个动点,过点 作直线 平行于 轴交 于点 ,交二次函数 的图象于点 .
(1)求二次函数的表达式;
(2)当以 、 、 为顶点的三角形与 相似时,求线段 的长度;
(3)已知点 是 轴上的点,若点 、 关于直线 对称,求点 的坐标.
已知正方形 与正方形 ,正方形 绕点 旋转一周.
(1)如图①,连接 、 ,求 的值;
(2)当正方形 旋转至图②位置时,连接 、 ,分别取 、 的中点 、 ,连接 、试探究: 与 的关系,并说明理由;
(3)连接 、 ,分别取 、 的中点 、 ,连接 , ,请直接写出线段 扫过的面积.

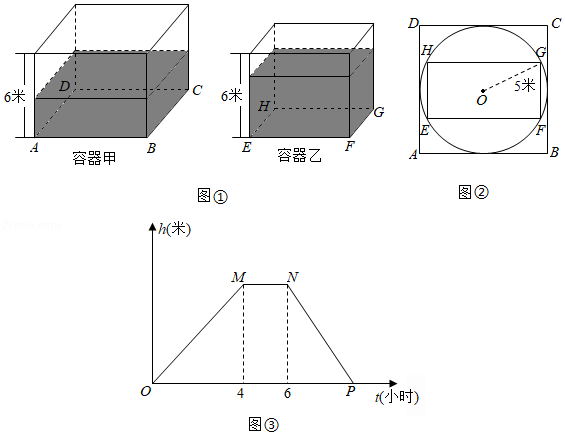
如图①,甲、乙都是高为6米的长方体容器,容器甲的底面 是正方形,容器乙的底面 是矩形.如图②,已知正方形 与矩形 满足如下条件:正方形 外切于一个半径为5米的圆 ,矩形 内接于这个圆 , .
(1)求容器甲、乙的容积分别为多少立方米?
(2)现在我们分别向容器甲、乙同时持续注水(注水前两个容器是空的),一开始注水流量均为25立方米 小时,4小时后,把容器甲的注水流量增加 立方米 小时,同时保持容器乙的注水流量不变,继续注水2小时后,把容器甲的注水流量再一次增加50立方米 小时,同时容器乙的注水流量仍旧保持不变,直到两个容器的水位高度相同,停止注水.在整个注水过程中,当注水时间为 时,我们把容器甲的水位高度记为 ,容器乙的水位高度记为 ,设 ,已知 (米 关于注水时间 (小时)的函数图象如图③所示,其中 平行于横轴,根据图中所给信息,解决下列问题:
①求 的值;
②求图③中线段 所在直线的解析式.
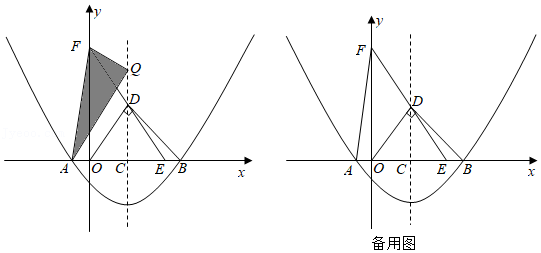
如图,二次函数 是实数,且 的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴与 轴交于点 .已知点 位于第一象限,且在对称轴上, ,点 在 轴的正半轴上, ,连接 并延长交 轴于点 ,连接 .
(1)求 、 、 三点的坐标(用数字或含 的式子表示);
(2)已知点 在抛物线的对称轴上,当 的周长的最小值等于 时,求 的值.
已知二次函数 的图象经过 , 两点.
(1)求 的值;
(2)当 时,该函数的图象的顶点的纵坐标的最小值是 1 .
(3)设 是该函数的图象与 轴的一个公共点.当 时,结合函数的图象,直接写出 的取值范围.
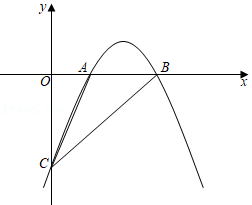
如图,抛物线 与 轴交于点 、 ,与 轴交于点 ,已知 .
(1)求 的值和直线 对应的函数表达式;
(2) 为抛物线上一点,若 ,请直接写出点 的坐标;
(3) 为抛物线上一点,若 ,求点 的坐标.
在平面直角坐标系 中,对于 、 两点,若在 轴上存在点 ,使得 ,且 ,则称 、 两点互相关联,把其中一个点叫做另一个点的关联点.已知点 、 ,点 在一次函数 的图象上.
(1)①如图,在点 、 、 中,点 的关联点是 (填" "、" "或" " ;
②若在线段 上存在点 的关联点 ,则点 的坐标是 ;
(2)若在线段 上存在点 的关联点 ,求实数 的取值范围;
(3)分别以点 、 为圆心,1为半径作 、 .若对 上的任意一点 ,在 上总存在点 ,使得 、 两点互相关联,请写出点 的坐标.

【阅读】
通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是"数形结合"思想的典型应用.
【理解】
(1)如图1, , ,垂足分别为 、 , 是 的中点,连接 .已知 , .
①分别求线段 、 的长(用含 、 的代数式表示);
②比较大小: (填" "、" "或" " ,并用含 、 的代数式表示该大小关系.
【应用】
(2)如图2,在平面直角坐标系 中,点 、 在反比例函数 的图象上,横坐标分别为 、 .设 , ,记 .
①当 , 时, ;当 , 时, ;
②通过归纳猜想,可得 的最小值是 .请根据图2构造恰当的图形,并说明你的猜想成立.

如图,在矩形 中, , .动点 从点 出发沿折线 向终点 运动,在边 上以 的速度运动;在边 上以 的速度运动,过点 作线段 与射线 相交于点 ,且 ,连接 , .设点 的运动时间为 , 与 重合部分图形的面积为 .
(1)当点 与点 重合时,直接写出 的长;
(2)当点 在边 上运动时,直接写出 的长(用含 的代数式表示);
(3)求
关于
的函数解析式,并写出自变量
的取值范围.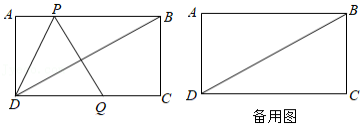
如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .

(1)若 .直接写出 的长(用含 的代数式表示);
(2)若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如②,判断四边形 的形状,并说明理由;
(3)若 ,直接写出 的度数.
如图,在 中, , , ,点 为边 的中点.动点 从点 出发,沿折线 以每秒1个单位长度的速度向点 运动,当点 不与点 、 重合时,连结 .作点 关于直线 的对称点 ,连结 、 .设点 的运动时间为 秒.
(1)线段 的长为 ;
(2)用含 的代数式表示线段 的长;
(3)当点 在 内部时,求 的取值范围;
(4)当 与 相等时,直接写出 的值.

实践与探究
操作一:如图①,已知正方形纸片 ,将正方形纸片沿过点 的直线折叠,使点 落在正方形 的内部,点 的对应点为点 ,折痕为 ,再将纸片沿过点 的直线折叠,使 与 重合,折痕为 ,则 度.
操作二:如图②,将正方形纸片沿 继续折叠,点 的对应点为点 .我们发现,当点 的位置不同时,点 的位置也不同.当点 在 边的某一位置时,点 恰好落在折痕 上,则 度.
在图②中,运用以上操作所得结论,解答下列问题:
(1)设 与 的交点为点 .求证: ;
(2)若 ,则线段 的长为 .
