在平面直角坐标系 中,对于 、 两点,若在 轴上存在点 ,使得 ,且 ,则称 、 两点互相关联,把其中一个点叫做另一个点的关联点.已知点 、 ,点 在一次函数 的图象上.
(1)①如图,在点 、 、 中,点 的关联点是 (填" "、" "或" " ;
②若在线段 上存在点 的关联点 ,则点 的坐标是 ;
(2)若在线段 上存在点 的关联点 ,求实数 的取值范围;
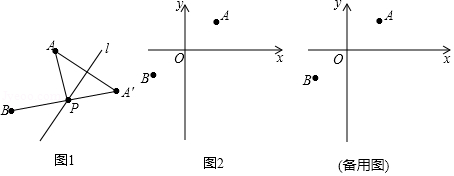
(3)分别以点 、 为圆心,1为半径作 、 .若对 上的任意一点 ,在 上总存在点 ,使得 、 两点互相关联,请写出点 的坐标.
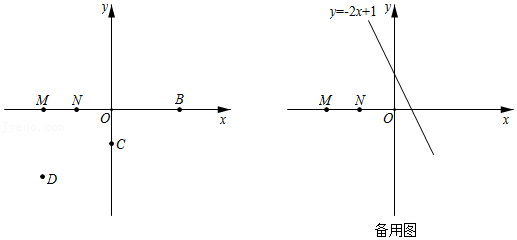
相关知识点
推荐套卷



 粤公网安备 44130202000953号
粤公网安备 44130202000953号