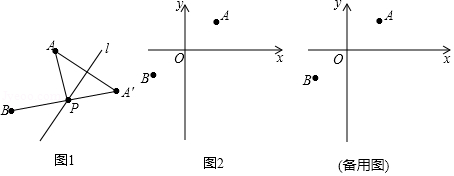
【定义】如图1, , 为直线 同侧的两点,过点 作直线 的对称点 ,连接 交直线 于点 ,连接 ,则称点 为点 , 关于直线 的“等角点”.
【运用】如图2,在平面直角坐标系 中,已知 , 两点.
(1) , , 三点中,点 是点 , 关于直线 的等角点;
(2)若直线 垂直于 轴,点 是点 , 关于直线 的等角点,其中 , ,求证: ;
(3)若点 是点 , 关于直线 的等角点,且点 位于直线 的右下方,当 时,求 的取值范围(直接写出结果).
推荐套卷
【定义】如图1, , 为直线 同侧的两点,过点 作直线 的对称点 ,连接 交直线 于点 ,连接 ,则称点 为点 , 关于直线 的“等角点”.
【运用】如图2,在平面直角坐标系 中,已知 , 两点.
(1) , , 三点中,点 是点 , 关于直线 的等角点;
(2)若直线 垂直于 轴,点 是点 , 关于直线 的等角点,其中 , ,求证: ;
(3)若点 是点 , 关于直线 的等角点,且点 位于直线 的右下方,当 时,求 的取值范围(直接写出结果).
