如图1,在四边形 中, ,点 在边 上,且 , ,作 交线段 于点 ,连接 .
(1)求证: ;
(2)如图2.若 , , ,求 的长;
(3)如图3,若 的延长线经过 的中点 ,求 的值.

已知抛物线 的对称轴为直线 .
(1)求 的值;
(2)若点 , , , 都在此抛物线上,且 , .比较 与 的大小,并说明理由;
(3)设直线 与抛物线 交于点 、 ,与抛物线 交于点 , ,求线段 与线段 的长度之比.
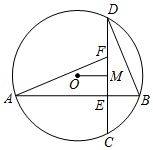
如图,圆 中两条互相垂直的弦 , 交于点 .
(1) 是 的中点, , ,求圆 的半径长;
(2)点 在 上,且 ,求证: .
某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
观察思考
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图 ;当正方形地砖有2块时,等腰直角三角形地砖有8块(如图 ;以此类推.

规律总结
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有 为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含 的代数式表示).
问题解决
(3)现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
已知,在 中, , .

(1)如图1,已知点 在 边上, , ,连结 .试探究 与 的关系;
(2)如图2,已知点 在 下方, , ,连结 .若 , , , 交 于点 ,求 的长;
(3)如图3,已知点 在 下方,连结 、 、 .若 , , , ,求 的值.
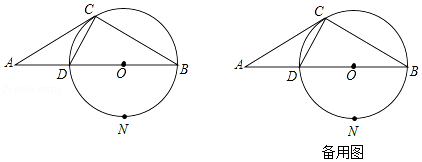
如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

如图,在 中, 是直径, 是弦, ,垂足为 ,过点 的 的切线与 延长线交于点 ,连接 .
(1)求证: 为 的切线;
(2)若 半径为3, ,求 .

如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
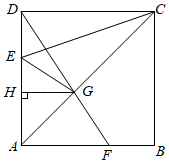
如图,点 在正方形 边 上,点 是线段 上的动点(不与点 重合), 交 于点 , 于点 , , .
(1)求 ;
(2)设 , ,试探究 与 的函数关系式(写出 的取值范围);
(3)当 时,判断 与 的位置关系并说明理由.
超市购进某种苹果,如果进价增加2元 千克要用300元;如果进价减少2元 千克,同样数量的苹果只用200元.
(1)求苹果的进价;
(2)如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元 千克,写出购进苹果的支出 (元 与购进数量 (千克)之间的函数关系式;
(3)超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完,据统计,销售单价 (元 千克)与一天销售数量 (千克)的关系为 .在(2)的条件下,要使超市销售苹果利润 (元 最大,求一天购进苹果数量.(利润 销售收入 购进支出)
如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 , 是 的直径,连接 .
(1)求证: ;
(2)若 , 于点 , , ,求 的值.

如图,在 中, , 平分 交 于点 ,点 在 上, , 是 的外接圆,交 于点 .
(1)求证: 是 的切线;
(2)若 的半径为5, ,求 .

在等腰 中, ,点 是 边上一点(不与点 、 重合),连结 .
(1)如图1,若 ,点 关于直线 的对称点为点 ,连结 , ,则 ;
(2)若 ,将线段 绕点 顺时针旋转 得到线段 ,连结 .
①在图2中补全图形;
②探究 与 的数量关系,并证明;
(3)如图3,若 ,且 .试探究 、 、 之间满足的数量关系,并证明.

如图1,在 中, , ,点 是 边上一点(含端点 、 ,过点 作 垂直于射线 ,垂足为 ,点 在射线 上,且 ,连接 、 .

(1)求证: ;
(2)如图2,连接 ,点 、 、 分别为线段 、 、 的中点,连接 、 、 .求 的度数及 的值;
(3)在(2)的条件下,若 ,直接写出 面积的最大值.