实践与探究
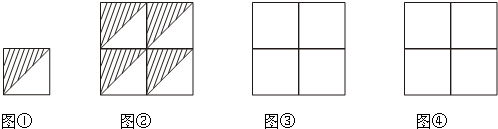
操作一：如图①，已知正方形纸片 ，将正方形纸片沿过点 的直线折叠，使点 落在正方形 的内部，点 的对应点为点 ，折痕为 ，再将纸片沿过点 的直线折叠，使 与 重合，折痕为 ，则 度．
操作二：如图②，将正方形纸片沿 继续折叠，点 的对应点为点 ．我们发现，当点 的位置不同时，点 的位置也不同．当点 在 边的某一位置时，点 恰好落在折痕 上，则 度．
在图②中，运用以上操作所得结论，解答下列问题：
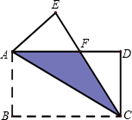
（1）设 与 的交点为点 ．求证： ；
（2）若 ，则线段 的长为 ．
相关试题
观察下列等式
，
，
，将以这三个等式两边分别相加得：
。
（1）猜想并写出：
_________
（2）直接写出下列各式的计算结果：
_________
（3）探究并计算：
某服装厂生产一种西装和领带，西装每套定价300元，领带每条定价50元。厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90％付款。现某客户要到该服装厂购买西装20套，领带x条（x＞20）。
（1）若该客户按方案①购买，需付款________元（用含x的代数式表示）；
若该客户按方案②购买，需付款________元（用含x的代数式表示）。
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？
②
,∴
其中
相关知识点
推荐套卷
粤公网安备 44130202000953号