如图,在菱形 中,对角线 与 相交于点 , , ,点 在边 上, ,连结 交 于点 .
(1)求 的长.
(2) 的值为 .

目前,国际上常用身体质量指数" "作为衡量人体健康状况的一个指标,其计算公式: 表示体重,单位:千克; 表示身高,单位:米).已知某区域成人的 数值标准为: 为瘦弱(不健康); 为偏瘦; 为正常; 为偏胖; 为肥胖(不健康).
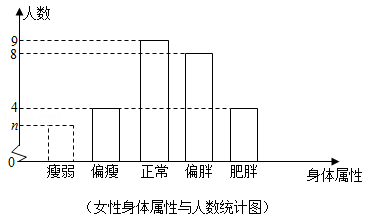
某研究人员从该区域的一体检中心随机抽取55名成人的体重、身高数据组成一个样本,计算每名成人的 数值后统计:
(男性身体属性与人数统计表)
| 身体属性 |
人数 |
| 瘦弱 |
2 |
| 偏瘦 |
2 |
| 正常 |
1 |
| 偏胖 |
9 |
| 肥胖 |
|
(1)求这个样本中身体属性为"正常"的人数;
(2)某女性的体重为51.2千克,身高为1.6米,求该女性的 数值;
(3)当 且 、 为正整数)时,求这个样本中身体属性为"不健康"的男性人数与身体属性为"不健康"的女性人数的比值.
将一物体(视为边长为 米的正方形 从地面 上挪到货车车厢内.如图所示,刚开始点 与斜面 上的点 重合,先将该物体绕点 (E)按逆时针方向旋转至正方形 的位置,再将其沿 方向平移至正方形 的位置(此时点 与点 重合),最后将物体移到车厢平台面 上.已知 , ,过点 作 于点 , 米, 米.
(1)求线段 的长度;
(2)求在此过程中点 运动至点 所经过的路程.

如图所示,在矩形 中,点 在线段 上,点 在线段 的延长线上,连接 交线段 于点 ,连接 ,若 .
(1)求证:四边形 是平行四边形;
(2)若 ,求线段 的长度.

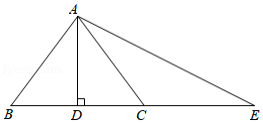
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
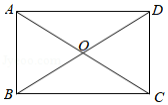
如图, 的对角线 , 相交于点 , 是等边三角形, .
(1)求证: 是矩形;
(2)求 的长.
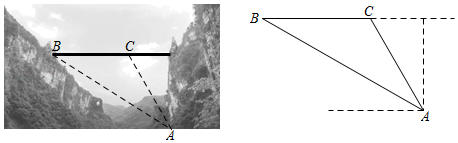
张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面 , 的仰角分别为 , ,测得 长为320米,求观测点 到桥面 的距离.(结果保留整数,参考数据:
如图,在 中, , ,以点 为圆心, 为半径的圆交 的延长线于点 ,过点 作 的平行线,交 于点 ,连接 .
(1)求证: 为 的切线;
(2)若 ,求弧 的长.

为了积极响应中共中央文明办关于"文明用餐"的倡议,某校开展了"你的家庭使用公筷了吗?"的调查活动,并随机抽取了部分学生,对他们家庭用餐使用公筷情况进行统计,统计分类为以下四种: (完全使用)、 (多数时间使用)、 (偶尔使用)、 (完全不使用),将数据进行整理后,绘制了两幅不完整的统计图.
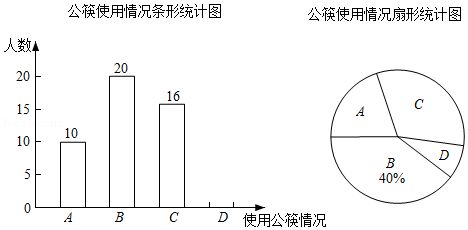
根据以上信息,解答下列问题:
(1)本次抽取的学生总人数共有 ;
(2)补全条形统计图;
(3)扇形统计图中 对应的扇形的圆心角度数是 ;
(4)为了了解少数学生完全不使用公筷的原因,学校决定从 组的学生中随机抽取两位进行回访,若 组中有3名男生,其余均为女生,请用列表法或画树状图的方法,求抽取的两位学生恰好是一男一女的概率.
如图,在矩形 中,对角线 与 相交于点 , ,对角线 所在的直线绕点 顺时针旋转角 ,所得的直线 分别交 , 于点 , .
(1)求证: ;
(2)当旋转角 为多少度时,四边形 为菱形?试说明理由.

星期天,小明与妈妈到离家 的洞庭湖博物馆参观.小明从家骑自行车先走, 后妈妈开车从家出发,沿相同路线前往博物馆,结果他们同时到达.已知妈妈开车的平均速度是小明骑自行车平均速度的4倍,求妈妈开车的平均速度.

如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
(1)求该反比例函数的表达式;
(2)若点 在 轴上,且 的面积为3,求点 的坐标.

如图,在四边形 中, , ,垂足分别为点 , .
(1)请你只添加一个条件(不另加辅助线),使得四边形 为平行四边形,你添加的条件是 ;
(2)添加了条件后,证明四边形 为平行四边形.

已知锐角 中,角 、 、 的对边分别为 、 、 ,边角总满足关系式: .

(1)如图1,若 , , ,求 的值;
(2)某公园准备在园内一个锐角三角形水池 中建一座小型景观桥 (如图2所示),若 , 米, 米, ,求景观桥 的长度.