如图,已知 是 外一点.用两种不同的方法过点 作 的一条切线.
要求:(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.

甲、乙两人沿同一直道从 地去 地.甲比乙早 出发,乙的速度是甲的2倍.在整个行程中,甲离 地的距离 (单位: 与时间 (单位: 之间的函数关系如图所示.
(1)在图中画出乙离 地的距离 (单位: 与时间 之间的函数图象;
(2)若甲比乙晚 到达 地,求甲整个行程所用的时间.

如图,为了测量河对岸两点 , 之间的距离,在河岸这边取点 , .测得 , , , , .设 , , , 在同一平面内,求 , 两点之间的距离.
(参考数据: , .

如图, 与 交于点 , , , 为 延长线上一点,过点 作 ,交 的延长线于点 .
(1)求证 ;
(2)若 , , ,求 的长.

我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端 离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点 到岸边 的距离;
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点 恰好位于海面.求点 到岸边 的距离.
(参考数据: , , , , ,
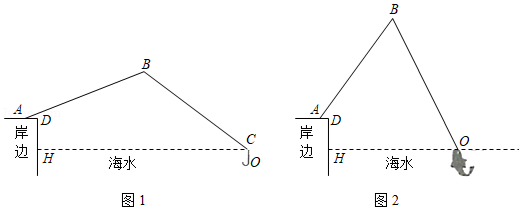
如图, 中, ,以点 为圆心, 为半径作 , 为 上一点,连接 、 , , 平分 .
(1)求证: 是 的切线;
(2)延长 、 相交于点 ,若 ,求 的值.
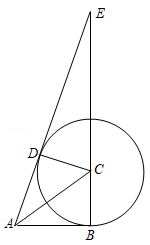
如图,点 是 的中点,四边形 是平行四边形.
(1)求证:四边形 是平行四边形;
(2)如果 ,求证:四边形 是矩形.
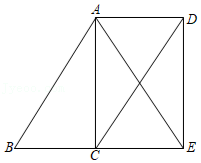
如图,在平面直角坐标系 中,一次函数 的图象分别与 轴、 轴交于点 、 ,与反比例函数 的图象交于点 ,连接 .已知点 , .
(1)求 、 的值;
(2)求 的面积.

如图, 、 、 、 是直线 上的四点, , , .
(1)求证: ;
(2)将 沿直线 翻折得到△ .
①用直尺和圆规在图中作出△ (保留作图痕迹,不要求写作法);
②连接 ,则直线 与 的位置关系是 .

疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过 天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数 (万人)与各自接种时间 (天 之间的关系如图所示.
(1)直接写出乙地每天接种的人数及 的值;
(2)当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.

数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南,北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线;
(2)如图, 是经过南、北极的圆,地球半径 约为 .弦 ,过点 作 于点 ,连接 .若 ,则以 为半径的圆的周长是北纬 纬线的长度;
(3)参考数据: 取3, , .
小组成员给出了如下解答,请你补充完整:
解:因为 , ,
所以 (填推理依据),
因为 ,所以 ,
在 中, .
(填" "或" " .
所以北纬 的纬线长 .
(填相应的三角形函数值)
(结果取整数).

如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)求反比例函数的解析式;
(2)求 的面积.
图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点 、 、 均为格点.只用无刻度的直尺,分别在给定的网格中找一格点 ,按下列要求作图:
(1)在图①中,连结 、 ,使 ;
(2)在图②中,连结 、 、 ,使 ;
(3)在图③中,连结 、 ,使 .
