江堤边发生管涌,江水不断涌到堤边一个原本干涸的池塘,假定每分钟涌出的水量相同,如果用两台抽水机抽水, 可以抽完池塘里的蓄水;如果用 台抽水机抽水, 可以抽完;如果要在 内将池塘里的蓄水抽完,那么至少需要抽水机多少台?
如图,在 中, , ,点 在 上, ,连接 , ,点 是边 上一动点(点 不与点 重合),过点 作 的垂线,与 相交于点 ,连接 ,设 , 与 重叠部分的面积为 .
(1)求 的长;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.

如图,三角形 内的线段 , 相交于点 ,已知 , .设 和四边形 的面积分别为 .
(1)求 的值;
(2)如果 ,求 的值.

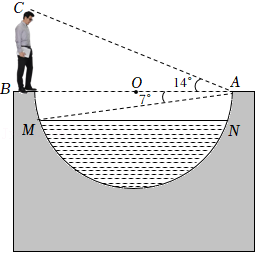
如图,某水渠的横断面是以 为直径的半圆 ,其中水面截线 .嘉琪在 处测得垂直站立于 处的爸爸头顶 的仰角为 ,点 的俯角为 .已知爸爸的身高为 .
(1)求 的大小及 的长;
(2)请在图中画出线段 ,用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).
(参考数据: 取 , 取 )
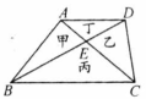
如图,四边形 被 与 分成甲、乙、丙、丁 个三角形,已知 ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?
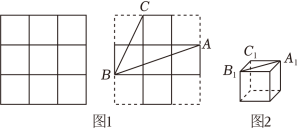
综合与实践
主题:制作无盖正方体形纸盒.
素材:一张正方形纸板.
步骤1:如图1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图2,把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:(1)直接写出纸板上 与纸盒上 的大小关系;
(2)证明(1)中你发现的结论.
王亮的爷爷今年(2012年) 周岁了,今年王亮的年龄恰好是他自己出生年份的各位数字之和,问王亮今年可能是多少周岁?
发现两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和.
验证 如, 为偶数.请把 的一半表示为两个正整数的平方和;
探究 设“发现”中的两个已知正整数为 ,请论证“发现”中的结论正确.
如图,莲花山是大连著名的景点之一.游客可以从山底乘坐索道车到达山顶,索道车运行的速度是 米/秒.小明要测量莲花山山顶白塔的高度,他在索道 处测得白塔底部 的仰角约为 ,测得白塔顶部 的仰角约为 ,索道车从 处运行到 处所用时间约为 分钟.
(1)索道车从 处运行到 处的距离约为_____米;
(2)请你利用小明测量的数据,求白塔BC的高度.(结果取整数)
(参考数据: , )

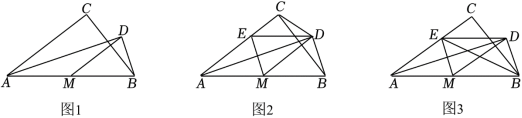
在 中, 是斜边 的中点,将线段 绕点 旋转至 位置,点 在直线 外,连接 .
(1)如图1,求 的大小;
(2)已知点 和边 上的点 满足 .
(i)如图2,连接 ,求证: ;
(ii)如图3,连接 ,若 ,求 的值.
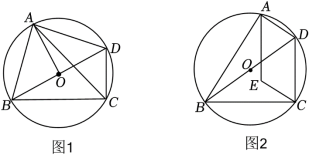
已知四边形 内接于 ,对角线 是 的直径.
(1)如图1,连接 ,若 ,求证: 平分 ;
(2)如图2, 为 内一点,满足 .若 , ,求弦 的长.
如图,三角形花园ABC紧邻湖泊,四边形ABDE是沿湖泊修建的人行步道.经测量,点C在点A的正东方向, .点E在点A的正北方向.点B,D在点C的正北方向, .点B在点A的北偏东30°,点D在点E的北偏东45°.
(1)求步道DE的长度(精确到个位);
(2)点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?
(参考数据: , )

为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为 分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
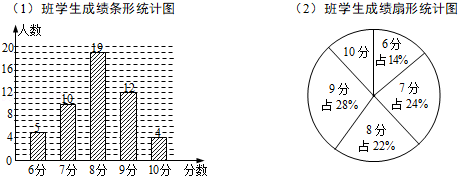
(1)求(2)班学生中测试成绩为 分的人数;
(2)请确定下表中 的值(只要求写出求 的计算过程);
|
统计量 |
平均数 |
众数 |
中位数 |
方差 |
|
(1)班 |
8 |
8 |
c |
1.16 |
|
(2)班 |
a |
b |
8 |
1.56 |
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.