2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站.如图中的照片展示了中国空间站上机械臂的一种工作状态.当两臂 ,两臂夹角 时,求 两点间的距离.(结果精确到 ,参考数据: )

为了解某初级中学落实《中共中央国务院关于全面加强新时代大中小学劳动教育的意见》的实施情况,调查组从该校全体学生中随机抽取部分学生,调查他们平均每周劳动时间 (单位: ),并对数据进行整理、描述和分析.以下是根据调查结果绘制的统计图表的一部分.
平均每周劳动时间频数统计表
|
平均每周劳动时间 |
频数 |
频率 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
合计 |
|
根据以上信息,回答下列问题:
(1)填空: _____, _____, _____;
(2)若该校有 名学生,请估计平均每周劳动时间在 范围内的学生人数.

为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为 千元/吨时,每天可售出 吨,每吨涨 千元,每天销量将减少 吨,据测算,每吨平均投入成本 千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于 千元,不高于 千元.请解答以下问题:
(1)求每天销量 (吨)与批发价 (千元/吨)之间的函数关系式,并直接写出自变量 的取值范围;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?
根据经营情况,公司对某商品在甲、乙两地的销售单价进行了如下调整:甲地上涨 ,乙地降价 元.已知销售单价调整前甲地比乙地少 元,调整后甲地比乙地少 元,求调整前甲、乙两地该商品的销售单价.
为了测量高速公路某桥的桥墩高度,某数学兴趣小组在同一水平地面 两处实地测量,如图所示.在 处测得桥墩顶部 处的仰角为 和桥墩底部 处的俯角为 ,在 处测得桥墩顶部 处的仰角为 ,测得 两点之间的距离为 ,直线 在同一平面内,请你用以上数据,计算桥墩 的高度.(结果保留整数,参考数据: , )
如图,在平面直角坐标系 中,抛物线 的顶点 在抛物线 上,直线 与抛物线 分别交于点 .
(1)求 的值;
(2)将 的纵坐标分别记为 ,设 ,若 的最大值为 ,则 的值是多少?
(3) 是 轴的正半轴上一点,且 的中点 恰好在抛物线 上.试探究:此时无论 为何负值,在 轴的负半轴上是否存在定点 ,使 总为直角?若存在,请求出点 的坐标;若不存在,请说明理由.

2021年7月,中共中央办公厅,国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某中学为了切实减轻学生作业负担,落实课后服务相关要求,开设了书法、摄影、篮球、足球、乒乓球五项课后服务活动,为了解学生的个性化需求,学校随机抽取了部分学生进行问卷调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图,请你根据给出的信息解答下列问题:

(1)求 的值并把条形统计图补充完整;
(2)若该校有 名学生,试估计该校参加“书法”活动的学生有多少人?
(3)结合调查信息,请你给该校课后服务活动项目开设方面提出一条合理化的建议.
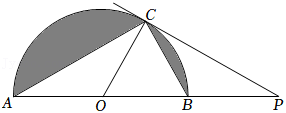
如图, 是圆 被直径 分成的半圆上一点,过点 的圆 的切线交 的延长线于点 ,连接 .
(1)求证: ;
(2)若 ,求 的度数;
(3)在(2)的条件下,若 ,求图中阴影部分的面积(结果保留 和根号).
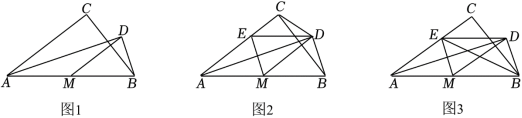
在 中, 是斜边 的中点,将线段 绕点 旋转至 位置,点 在直线 外,连接 .
(1)如图1,求 的大小;
(2)已知点 和边 上的点 满足 .
(i)如图2,连接 ,求证: ;
(ii)如图3,连接 ,若 ,求 的值.
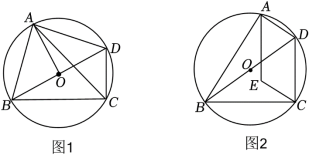
已知四边形 内接于 ,对角线 是 的直径.
(1)如图1,连接 ,若 ,求证: 平分 ;
(2)如图2, 为 内一点,满足 .若 , ,求弦 的长.
如图,三角形花园ABC紧邻湖泊,四边形ABDE是沿湖泊修建的人行步道.经测量,点C在点A的正东方向, .点E在点A的正北方向.点B,D在点C的正北方向, .点B在点A的北偏东30°,点D在点E的北偏东45°.
(1)求步道DE的长度(精确到个位);
(2)点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?
(参考数据: , )
