构建几何图形解决代数问题体现了“数形结合”的重要思想.在计算 时,如图所示,在 中, ,延长 使 ,连接 ,得 ,所以 .类比这种方法,计算 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 .若 ,则 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
抛物线 的一部分如图所示,设该抛物线与 轴的交点为 和 ,与 轴的交点为 ,若 ,则 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图所示, 是 的中位线, 为 上一点,且 的延长线交 于点 的延长线交 于点 ,则 等于( )

| A. |
|
B. |
|
C. |
|
D. |
|
已知抛物线 的顶点为 ,点 是第一象限内该二次函数图象上一点,过点 作 轴的平行线交二次函数图象于点 ,分别过点 作 轴的垂线,垂足分别为 ,连接 交 于点 与 ( )

| A. | 始终不相似 |
B. | 始终相似 |
| C. | 只有 时相似 |
D. | 无法确定 |
如图, 和 表示两根直立于地面的柱子, 和 表示起固定作用的两根钢筋, 与 相交于点 ,已知 ,则点 离地面的高度 为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,有一块锐角三角形材料,边 ,高 ,要把它加工成矩形零件,使其一边在 上,其余两个顶点分别在 上,且 ,则这个矩形零件的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
有一块锐角三角形余料 ,它的边 边上的高为 ,现要把它分割成若干个邻边长分别为 和 的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为 的边在 上,则按如图方式分割成的小长方形零件最多有 ( )

| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面 ( )

| A. |
|
B. |
|
C. |
|
D. |
|
由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连接 ,延长 交 于点 .若 ,则 的值为 ( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形 中, ,连接 ,以 为直径的圆交 于点 .若 ,则 的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
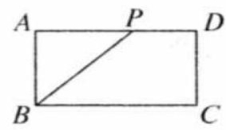
如图,已知在矩形 中, ,点 是 边上的一个动点,连接 ,点 关于直线 的对称点为 ,当点 运动时,点 也,随之运动.若点 从点 运动到点 ,则线段 扫过的区域的面积是( )
| A. |
|
B. |
|
C. |
|
D. |
|
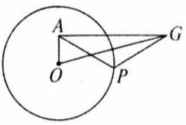
已知 的半径为 为圆内一定点, 为圆上一动点,以 为边作等腰 的最大值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
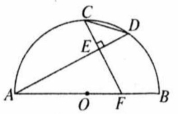
如图,点 是半圆 的中点, 是直径, 弦 于点 ,交 于点 ,若 ,则 的长为( )
| A. |
|
B. |
|
C. |
|
D. |
|