初中数学解直角三角形的应用-仰角俯角问题解答题

2018年4月12日，菏泽国际牡丹花会拉开帷幕，菏泽电视台用直升机航拍技术全程直播．如图，在直升机的镜头下，观测曹州牡丹园 $A$处的俯角为 $30°$， $B$处的俯角为 $45°$，如果此时直升机镜头 $C$处的高度 $\mathit{CD}$为200米，点 $A$、 $B$、 $D$在同一条直线上，则 $A$、 $B$两点间的距离为多少米？（结果保留根号）

如图，两座建筑物的水平距离 $\mathit{BC}$为 $60m$，从 $C$点测得 $A$点的仰角 $\alpha$为 $53°$，从 $A$点测得 $D$点的俯角 $\beta$为 $37°$，求两座建筑物的高度（参考数据： $\sin 37°\approx \frac{3}{5}$， $\cos 37°\approx \frac{4}{5}$， $\tan 37°\approx \frac{3}{4}$， $\sin 53°\approx \frac{4}{5}$， $\cos 53°\approx \frac{3}{5}$， $\tan 53°\approx \frac{4}{3})$．

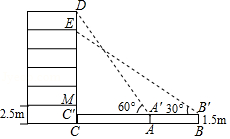
如图，某数学兴趣小组要测量一栋五层居民楼 $\mathit{CD}$的高度．该楼底层为车库，高2.5米；上面五层居住，每层高度相等．测角仪支架离地1.5米，在 $A$处测得五楼顶部点 $D$的仰角为 $60°$，在 $B$处测得四楼顶部点 $E$的仰角为 $30°$， $\mathit{AB}=14$米．求居民楼的高度（精确到0.1米，参考数据： $\sqrt{3}\approx 1.73)$

如图，两座建筑物的水平距离 $\mathit{BC}=30m$，从 $A$点测得 $D$点的俯角 $\alpha$为 $30°$，测得 $C$点的俯角 $\beta$为 $60°$，求这两座建筑物的高度．

耸立在临清市城北大运河东岸的舍利宝塔，是“运河四大名塔”之一（如图 $1)$．数学兴趣小组的小亮同学在塔上观景点 $P$处，利用测角仪测得运河两岸上的 $A$， $B$两点的俯角分别为 $17.9°$， $22°$，并测得塔底点 $C$到点 $B$的距离为142米 $(A$、 $B$、 $C$在同一直线上，如图 $2)$，求运河两岸上的 $A$、 $B$两点的距离（精确到1米）．

（参考数据： $\sin 22°\approx 0.37$， $\cos 22°\approx 0.93$， $\tan 22°\approx 0.40$， $\sin 17.9°\approx 0.31$， $\cos 17.9°\approx 0.95$， $\tan 17.9°\approx 0.32)$

某学校教学楼（甲楼）的顶部 $E$和大门 $A$之间挂了一些彩旗．小颖测得大门 $A$距甲楼的距离 $\mathit{AB}$是 $31m$，在 $A$处测得甲楼顶部 $E$处的仰角是 $31°$．

（1）求甲楼的高度及彩旗的长度；（精确到 $0.01m)$

（2）若小颖在甲楼楼底 $C$处测得学校后面医院楼（乙楼）楼顶 $G$处的仰角为 $40°$，爬到甲楼楼顶 $F$处测得乙楼楼顶 $G$处的仰角为 $19°$，求乙楼的高度及甲乙两楼之间的距离．（精确到 $0.01m)$

$(\cos 31°\approx 0.86$， $\tan 31°\approx 0.60$， $\cos 19°\approx 0.95$， $\tan 19°\approx 0.34$， $\cos 40°\approx 0.77$， $\tan 40°\approx 0.84)$

如图，某小区①号楼与⑪号楼隔河相望，李明家住在①号楼，他很想知道⑪号楼的高度，于是他做了一些测量，他先在 $B$点测得 $C$点的仰角为 $60°$，然后到42米高的楼顶 $A$处，测得 $C$点的仰角为 $30°$，请你帮助李明计算⑪号楼的高度 $\mathit{CD}$．

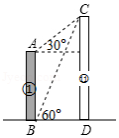
某数学小组开展测量物体高度的实践活动，他们要测量某建筑物上悬挂的电子显示屏的高度．如图所示，他们先在点 $A$测得电子显示屏底端点 $D$的仰角 $\angle \mathit{DAC}=15°$，然后向建筑物的方向前进 $10m$到达点 $B$，又测得电子显示屏顶端点 $E$的仰角 $\angle \mathit{EBC}=45°$，测得电子显示屏底端点 $D$的仰角 $\angle \mathit{DBC}=30°$．（点 $A$， $B$， $C$在同一条直线上，且与点 $D$， $E$在同一平面内，不考虑测角仪高度）

（1）求此时他们离建筑的距离 $\mathit{BC}$的长；

（2）求电子显示屏 $\mathit{DE}$的高度．

（以上结果用含根号的式子表示）

“五 $·$一”期间，小亮与家人到某旅游风景区登山，他们沿着坡度为 $5:12$的山坡 $\mathit{AB}$向上走了1300米，到达缆车站 $B$处，乘坐缆车到达山顶 $C$处，已知点 $A$、 $B$、 $C$、 $D$在同一平面内，从山脚 $A$处看山顶 $C$处的仰角为 $30°$，缆车行驶路线 $\mathit{BC}$与水平面的夹角为 $60°$，求山高 $\mathit{CD}$．（结果精确到1米， $\sqrt{3}\approx 1.732,\sqrt{2}\approx 1.414)$

（注 $:$坡度是指坡面的铅直高度与水平宽度的比）

某中学九年级数学兴趣小组想测量建筑物 $\mathit{AB}$的高度．他们在 $C$处仰望建筑物顶端，测得仰角为 $48°$，再往建筑物的方向前进6米到达 $D$处，测得仰角为 $64°$，求建筑物的高度．（测角器的高度忽略不计，结果精确到0.1米）

（参考数据： $\sin 48°\approx \frac{7}{10}$， $\tan 48°\approx \frac{11}{10}$， $\sin 64°\approx \frac{9}{10}$， $\tan 64°\approx 2)$

小明在热气球 $A$上看到正前方横跨河流两岸的大桥 $\mathit{BC}$，并测得 $B$， $C$两点的俯角分别为 $53°$和 $45°$，已知大桥 $\mathit{BC}$与地面在同一水平面上，其长度为 $75m$，请求出热气球离地面的高度．（参考数据： $\sin 53°\approx \frac{4}{5}$， $\cos 53°\approx \frac{3}{5}$， $\tan 53°\approx \frac{4}{3})$．

如图， $\mathit{AB}$是某景区内高 $10m$的观景台， $\mathit{CD}$是与 $\mathit{AB}$底部相平的一座雕像（含底座），在观景台顶 $A$处测得雕像顶 $C$点的仰角为 $30°$，从观景台底部 $B$处向雕像方向水平前进 $6m$到达点 $E$，在 $E$处测得雕像顶 $C$点的仰角为 $60°$，已知雕像底座 $\mathit{DF}$高 $8m$，求雕像 $\mathit{CF}$的高．（结果保留根号）

如图，聪聪想在自己家的窗口 $A$处测量对面建筑物 $\mathit{CD}$的高度，他首先量出窗口 $A$到地面的距离 $\left(\mathit{AB}\right)$为 $16m$，又测得从 $A$处看建筑物底部 $C$的俯角 $\alpha$为 $30°$，看建筑物顶部 $D$的仰角 $\beta$为 $53°$，且 $\mathit{AB}$， $\mathit{CD}$都与地面垂直，点 $A$， $B$， $C$， $D$在同一平面内．

（1）求 $\mathit{AB}$与 $\mathit{CD}$之间的距离（结果保留根号）．

（2）求建筑物 $\mathit{CD}$的高度（结果精确到 $1m)$．

（参考数据： $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6$， $\tan 53\approx 1.3$， $\sqrt{3}\approx 1.7)$

如图，某学校体育场看台的顶端 $C$到地面的垂直距离 $\mathit{CD}$为 $2m$，看台所在斜坡 $\mathit{CM}$的坡比 $i=1:3$，在点 $C$处测得旗杆顶点 $A$的仰角为 $30°$，在点 $M$处测得旗杆顶点 $A$的仰角为 $60°$，且 $B$， $M$， $D$三点在同一水平线上，求旗杆 $\mathit{AB}$的高度．（结果精确到 $0.1m$，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}=1.73)$

如图，学校教学楼上悬挂一块长为 $3m$的标语牌，即 $\mathit{CD}=3m$．数学活动课上，小明和小红要测量标语牌的底部点 $D$到地面的距离．测角仪支架高 $\mathit{AE}=\mathit{BF}=1.2m$，小明在 $E$处测得标语牌底部点 $D$的仰角为 $31°$，小红在 $F$处测得标语牌顶部点 $C$的仰角为 $45°$， $\mathit{AB}=5m$，依据他们测量的数据能否求出标语牌底部点 $D$到地面的距离 $\mathit{DH}$的长？若能，请计算；若不能，请说明理由（图中点 $A$， $B$， $C$， $D$， $E$， $F$， $H$在同一平面内）

（参考数据： $\tan 31°\approx 0.60$， $\sin 31°\approx 0.52$， $\cos 31°\approx 0.86)$