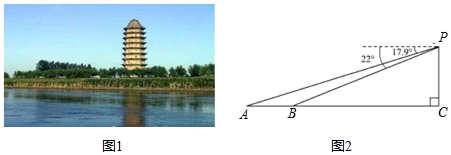
耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图 .数学兴趣小组的小亮同学在塔上观景点 处,利用测角仪测得运河两岸上的 , 两点的俯角分别为 , ,并测得塔底点 到点 的距离为142米 、 、 在同一直线上,如图 ,求运河两岸上的 、 两点的距离(精确到1米).
(参考数据:
,
,
,
,
,
相关知识点
推荐套卷
耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图 .数学兴趣小组的小亮同学在塔上观景点 处,利用测角仪测得运河两岸上的 , 两点的俯角分别为 , ,并测得塔底点 到点 的距离为142米 、 、 在同一直线上,如图 ,求运河两岸上的 、 两点的距离(精确到1米).
(参考数据:
,
,
,
,
,
