如图,为了测得一棵树的高度 ,小明在 处用高为 的测角仪 ,测得树顶 的仰角为 ,再向树方向前进 ,又测得树顶 的仰角为 ,求这棵树的高度 .

如图,在水平地面上有一幢房屋 与一棵树 ,在地面观测点 处测得屋顶 与树梢 的仰角分别是 与 , ,在屋顶 处测得 .若房屋的高 米,求树高 的长度.
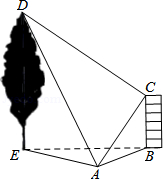
如图, 和 两幢楼地面距离 为 米,楼 高30米,从楼 的顶部点 测得楼 的顶部点 的仰角为 .
(1)求 的大小;
(2)求楼 的高度(结果保留根号).

在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点 垂直起飞到达点 处,测得1号楼顶部 的俯角为 ,测得2号楼顶部 的俯角为 ,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且 和 分别垂直地面于点 和 ,点 为 的中点,求2号楼的高度.(结果精确到
(参考数据 , , , , ,

某数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔 ,如图所示.在山脚平地上的 处测得塔底 的仰角为 ,向小山前进80米到达点 处,测得塔顶 的仰角为 ,求小山 的高度.

热气球的探测器显示,从热气球 处看大楼 顶部 的仰角为 ,看大楼底部 的俯角为 ,热气球与该楼的水平距离 为60米,求大楼 的高度.(结果精确到1米,参考数据:

成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台 处的高度,某数学兴趣小组在电视塔附近一建筑物楼项 处测得塔 处的仰角为 ,塔底部 处的俯角为 .已知建筑物的高 约为61米,请计算观景台的高 的值.
(结果精确到1米;参考数据: , ,
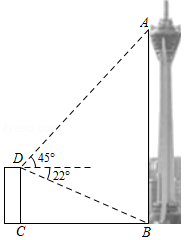
如图,线段 、 分别表示甲、乙两建筑物的高, , ,垂足分别为 、 .从 点测到 点的仰角 为 ,从 点测得 点的仰角 为 ,甲建筑物的高 米.
(1)求甲、乙两建筑物之间的距离 .
(2)求乙建筑物的高 .

如图,小明在 处测得风筝 处)的仰角为 ,同时在 正对着风筝方向距 处30米的 处,小明测得风筝的仰角为 ,求风筝此时的高度.(结果保留根号)

如图,两座建筑物 与 ,其地面距离 为 ,从 的顶点 测得 顶部 的仰角 ,测得其底部 的俯角 ,求建筑物 的高(结果保留根号)

某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚 到山腰 沿斜坡已建成步行道,为方便游客登顶观景,欲从 到 修建电动扶梯,经测量,山高 米,步行道 米, ,在 处测得山顶 的仰角为 .求电动扶梯 的长(结果保留根号).

如图, 、 两个小岛相距 ,一架直升飞机由 岛飞往 岛,其飞行高度一直保持在海平面以上的 ,当直升机飞到 处时,由 处测得 岛和 岛的俯角分别是 和 ,已知 、 、 和海平面上一点 都在同一个平面上,且 位于 的正下方,求 (结果取整数,

如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中 为下水管道口直径, 为可绕转轴 自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径 , 为检修时阀门开启的位置,且 .
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中 的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达 位置时,在点 处测得俯角 ,若此时点 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
, , , , , ,

随着我市农产品整体品牌形象“聊 胜一筹 ”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段 , 分别表示大棚的墙高和跨度, 表示保温板的长.已知墙高 为2米,墙面与保温板所成的角 ,在点 处测得 点、 点的仰角分别为 , ,如图2.求保温板 的长是多少米?(精确到0.1米)
(参考数据: , , , , , ,
