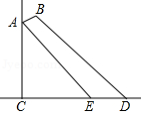
在小水池旁有一盏路灯,已知支架 的长是 , 端到地面的距离 是 ,支架 与灯柱 的夹角为 .小明在水池的外沿 测得支架 端的仰角是 ,在水池的内沿 测得支架 端的仰角是 (点 、 、 在同一直线上),求小水池的宽 .(结果精确到 , ,
相关知识点
推荐套卷
在小水池旁有一盏路灯,已知支架 的长是 , 端到地面的距离 是 ,支架 与灯柱 的夹角为 .小明在水池的外沿 测得支架 端的仰角是 ,在水池的内沿 测得支架 端的仰角是 (点 、 、 在同一直线上),求小水池的宽 .(结果精确到 , ,
