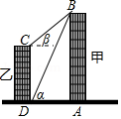
如图,线段 、 分别表示甲、乙两建筑物的高, , ,垂足分别为 、 .从 点测到 点的仰角 为 ,从 点测得 点的仰角 为 ,甲建筑物的高 米.
(1)求甲、乙两建筑物之间的距离 .
(2)求乙建筑物的高 .
相关知识点
推荐套卷
如图,线段 、 分别表示甲、乙两建筑物的高, , ,垂足分别为 、 .从 点测到 点的仰角 为 ,从 点测得 点的仰角 为 ,甲建筑物的高 米.
(1)求甲、乙两建筑物之间的距离 .
(2)求乙建筑物的高 .
