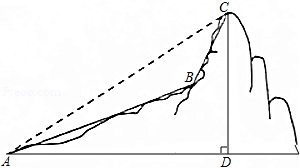
“五 一”期间,小亮与家人到某旅游风景区登山,他们沿着坡度为 的山坡 向上走了1300米,到达缆车站 处,乘坐缆车到达山顶 处,已知点 、 、 、 在同一平面内,从山脚 处看山顶 处的仰角为 ,缆车行驶路线 与水平面的夹角为 ,求山高 .(结果精确到1米,
(注 坡度是指坡面的铅直高度与水平宽度的比)
相关知识点
推荐套卷
“五 一”期间,小亮与家人到某旅游风景区登山,他们沿着坡度为 的山坡 向上走了1300米,到达缆车站 处,乘坐缆车到达山顶 处,已知点 、 、 、 在同一平面内,从山脚 处看山顶 处的仰角为 ,缆车行驶路线 与水平面的夹角为 ,求山高 .(结果精确到1米,
(注 坡度是指坡面的铅直高度与水平宽度的比)
