初中数学相似三角形的判定与性质解答题

如图，在中，，点在上，以线段的长为半径的与相切于点，分别交、于点、，连接并延长，交的延长线于点．

（1）求证：．

（2）已知的半径为3．

①若，则　　．

②当　　时，四边形为菱形．

如图，小明在笔直的河岸上的点处，以正对岸明显的标志点为参照点，设计出两种测量河宽的方案，绘制了相应的示意图，并用测角仪、卷尺及标杆测得一些数据如下：

（1）请你选择一种方案，结合示意图，简述测量过程；

（2）按照你选定的方案，求河宽．（参考数据：，

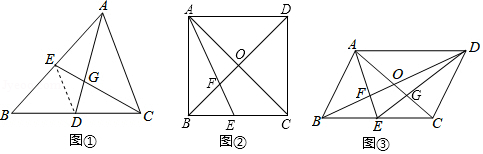
教材呈现：如图是华师版九年级上册数学教材第78页的部分内容．

例2 如图，在中，，分别是边，的中点，，相交于点，求证：

证明：连结．

请根据教材提示，结合图①，写出完整的证明过程．

结论应用：在中，对角线、交于点，为边的中点，、交于点．

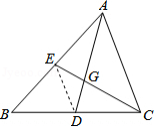
（1）如图②，若为正方形，且，则的长为　　．

（2）如图③，连结交于点，若四边形的面积为，则的面积为　　．

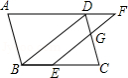
如图，在中，点在边上，点在边的延长线上，且，与交于点．

（1）求证：；

（2）若，，求的长．

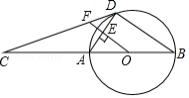
如图，为的直径，为延长线上一点，是的切线，为切点，于点，交于点．

（1）求证：；

（2）若，，求的长．

如图1，△ABC中，BC=25，BC边上的高为20，将AB，AC分别n等分，连接两边对应的等分点，以这些连接线为一边做矩形，使这些矩形的边B₁C₁,B₂C₂,B₃C₃……的对应边分别为 B₂C₂,B₃C₃,B₄C₄……

（1）若n=5，如图2，求B₃C₃为一边的矩形的面积；
（2）若n=5，求所有矩形的面积和；
（3）当分为n等分时，你能用含有n的表达式表示所有矩形的面积和吗？

如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则的值为          ．

如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

阅读：如图1，在△ABC中，BE是AC边上的中线， D是BC边上的一点，CD：BD=1：2，AD与BE相交于点P，求的值．小昊发现，过点A作AF∥BC，交BE的延长线于点F，通过构造△AEF，经过推理和计算能够使问题得到解决（如图2）．

（1）的值为          ；
（2）参考小昊思考问题的方法，解决问题：
如图3，在△ABC中，∠ACB=90°，点D在BC的延长线上，AD与AC边上的中线BE的延长线交于点P，DC：BC：AC=1：2：3．

求的值；
若CD=2，求BP的长．

如图，已知点D是△ABC的边AC上的一点，连接BD．∠ABD＝∠C，AB＝6，AD＝4．

（1）求证：△ABD∽△ACB；
（2）求线段CD的长．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

基本模型
如图1，点A，F，B在同一直线上，若∠A=∠B=∠EFC=90°，易得△AFE∽△BCF．
（1）模型拓展：
如图2，点A，F，B在同一直线上，若∠A=∠B=∠EFC，求证：△AFE∽△BCF；
（2）拓展应用：如图3，AB是半圆⊙O的直径，弦长AC=BC=4，E，F分别是AC，AB上的一点，若∠CFE=45°．若设AE=y，BF=x，求出y与x的函数关系式及y的最大值；

如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

（年青海省西宁市）如图，已知BC为⊙O的直径，BA平分∠FBC交⊙O于点A，D是射线BF上的一点，且满足，过点O作OM⊥AC于点E，交⊙O于点M，连接BM，AM．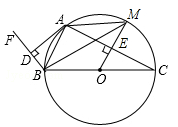

（1）求证：AD是⊙O的切线；
（2）若sin∠ABM=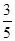，AM=6，求⊙O的半径．

（年贵州省遵义市）如图，△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD、DE．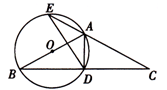

（1）求证：D是BC的中点；
（2）若DE=3，BD—AD=2，求⊙O的半径；
（3）在（2）的条件下，求弦AE的长．