如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D, ,求 的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.

某学习小组的学生在学习中遇到了下面的问题:
如图1,在
和
中,
,
,点
,
,
在同一条直线上,连接
,点
是
的中点,连接
,
,试判断
的形状并说明理由.
问题探究:
(1)小婷同学提出解题思路:先探究 的两条边是否相等,如 ,以下是她的证明过程
证明:延长线段 交 的延长线于点 . 是 的中点, . , . |
. 又 , . . . |
请根据以上证明过程,解答下列两个问题:
①在图1中作出证明中所描述的辅助线;
②在证明的括号中填写理由(请在 , , , 中选择).
(2)在(1)的探究结论的基础上,请你帮助小婷求出 的度数,并判断 的形状.
问题拓展:
(3)如图2,当 绕点 逆时针旋转某个角度时,连接 ,延长 交 的延长线于点 ,其他条件不变,判断 的形状并给出证明.
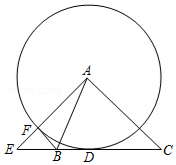
如图,已知 AD是△ ABC的外角∠ EAC的平分线,交 BC的延长线于点 D,延长 DA交△ ABC的外接圆于点 F,连接 FB, FC.
(1)求证:∠ FBC=∠ FCB;
(2)已知 FA• FD=12,若 AB是△ ABC外接圆的直径, FA=2,求 CD的长.

如图,在正方形 中,点 在 边上,连接 , 的平分线 与 边交于点 ,与 的延长线交于点 .设 .
(1)若 , ,求线段 的长.
(2)连接 ,若 ,
①求证:点 为 边的中点.
②求 的值.

如图,一次函数 y=﹣ x+1的图象与 x轴、 y轴分别交于点 A、 B,以线段 AB为边在第一象限作等边△ ABC.
(1)若点 C在反比例函数 y= 的图象上,求该反比例函数的解析式;
(2)点 P(2 , m)在第一象限,过点 P作 x轴的垂线,垂足为 D,当△ PAD与△ OAB相似时, P点是否在(1)中反比例函数图象上?如果在,求出 P点坐标;如果不在,请加以说明.

正方形 的边长为 ,点 、 分别是线段 、 上的动点,连接 并延长,交边 于 ,过 作 ,垂足为 ,交边 于点 .

(1)如图1,若点 与点 重合,求证: ;
(2)如图2,若点 从点 出发,以 的速度沿 向点 运动,同时点 从点 出发,以 的速度沿 向点 运动,运动时间为 .
①设 ,求 关于 的函数表达式;
②当 时,连接 ,求 的长.
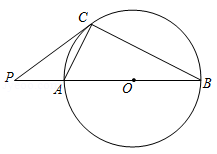
如图, 是 上一点,点 在直径 的延长线上, 的半径为3, , .
(1)求证: 是 的切线.
(2)求 的值.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图,在四边形 中, ,过点 作 于 ,若 .
(1)求证: ;
(2)连接 交 于点 ,若 , ,求 的长.

阅读与思考
请阅读下列科普材料,并完成相应的任务.
图算法 图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系: 得出,当 时, .但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种根据特制的线条进行计算的方法就是图算法. 再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少? 我们可以根据公式 求得 的值,也可以设计一种图算法直接得出结果:我们先来画出一个 的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值. 图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性. |
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性:
①用公式 计算:当 , 时, 的值为多少;
②如图,在 中, , 是 的角平分线, , ,用你所学的几何知识求线段 的长.

如图, 为线段 上一点,以 为圆心, 长为半径的 交 于点 ,点 在 上,连接 ,满足 .
(1)求证: 是 的切线;
(2)若 ,求 的值.
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图, 是 的平分线,点 在 上,以 为直径的 交 于点 ,过点 作 的垂线,垂足为点 ,交 于点 .
(1)求证:直线 是 的切线;
(2)若 ,设 的半径为 ,求 的长度.
