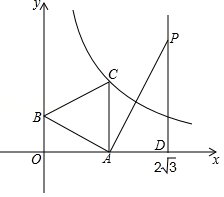
如图，一次函数 y＝﹣ x+1的图象与 x轴、 y轴分别交于点 A、 B，以线段 AB为边在第一象限作等边△ ABC．
（1）若点 C在反比例函数 y＝ 的图象上，求该反比例函数的解析式；
（2）点 P（2 ， m）在第一象限，过点 P作 x轴的垂线，垂足为 D，当△ PAD与△ OAB相似时， P点是否在（1）中反比例函数图象上？如果在，求出 P点坐标；如果不在，请加以说明．
相关试题
.
.
,并求当x=2，y=1时，代数式的值.
肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同。小明喜欢
向上代表红枣馅，连续抛掷这个骰子两次表示随机推荐套卷
如图，一次函数 y＝﹣ x+1的图象与 x轴、 y轴分别交于点 A、 B，以线段 AB为边在第一象限作等边△ ABC．
（1）若点 C在反比例函数 y＝ 的图象上，求该反比例函数的解析式；
（2）点 P（2 ， m）在第一象限，过点 P作 x轴的垂线，垂足为 D，当△ PAD与△ OAB相似时， P点是否在（1）中反比例函数图象上？如果在，求出 P点坐标；如果不在，请加以说明．
粤公网安备 44130202000953号