如图,在中,
,以
为直径的
交
边于点
,过点
作
,与过点
的切线交于点
,连接
.
(1)求证:;
(2)若,
,求
的长.

如图,为半圆
的直径,点
为半圆上任一点.
(1)若,过点
作半圆
的切线交直线
于点
.求证:
;
(2)若,过点
作
的平行线交半圆
于点
.当以点
,
,
,
为顶点的四边形为菱形时,求
的长.

如图,是
的直径,
切
于点
,
交
于点
.已知
的半径为6,
.
(1)求的度数.
(2)求的长.(结果保留
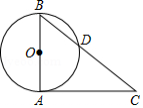
如图,,
为
中点,点
在线段
上(不与点
,
重合),将
绕点
逆时针旋转
后得到扇形
,
,
分别切优弧
于点
,
,且点
,
在
异侧,连接
.
(1)求证:;
(2)当时,求
的长(结果保留
;
(3)若的外心在扇形
的内部,求
的取值范围.

如图,是
的直径,过
外一点
作
的两条切线
,
,切点分别为
,
,连接
,
.
(1)求证:;
(2)连接,
,若
,
,
,求
的长.

如图,是
的一条弦,
是
的中点,过点
作
于点
,过点
作
的切线交
的延长线于点
.
(1)求证:;
(2)若,
,求
的半径.
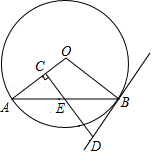
如图, 为 的直径, 为弦 的中点,连接 并延长交 于点 ,过点 作 的切线,交 的延长线于点 .
(1)求证: ;
(2)连接 ,若 ,写出求四边形 面积的思路.

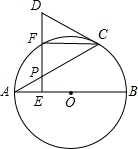
如图, 是 的直径,点 是弦 上一动点(不与 , 重合),过点 作 ,垂足为 ,射线 交 于点 ,交过点 的切线于点 .
(1)求证: ;
(2)若 ,当 是 的中点时,判断以 , , , 为顶点的四边形是什么特殊四边形?说明理由.
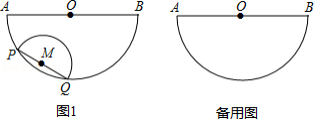
如图,半圆 的直径 ,以长为2的弦 为直径,向点 方向作半圆 ,其中 点在 上且不与 点重合,但 点可与 点重合.
发现: 的长与 的长之和为定值 ,求
思考:点 与 的最大距离为 ,此时点 , 间的距离为 ;
点 与 的最小距离为 ,此时半圆 的弧与 所围成的封闭图形面积为 ;
探究:当半圆 与 相切时,求 的长.
(注:结果保留 , ,
如图,为
的直径,
为
延长线上一点,
是
的切线,
为切点,
于点
,交
于点
.
(1)求证:;
(2)若,
,求
的长.
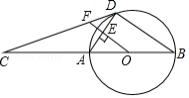
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D已知经过点D的⊙O切线恰好经过点C

(1)试判断CD与AC的位置关系,并证明;
(2)若△ACB∽△CDB,且AC=3,求图中阴影部分的面积
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.
(1)求证:△ADE是等腰三角形;
(2)若AD=2 ,求BE的长.
,求BE的长.
(年贵州省遵义市)如图,抛物线 (
( ≠0)与
≠0)与 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与 轴交与点C(0,2).
轴交与点C(0,2).

(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;(解题用图见答题卡)
(3)以AB为直径作⊙M,直线经过点E(-1,-5),并且与⊙M相切,求该直线的解析式.(解题用图见答题卡)
(年青海省中考)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.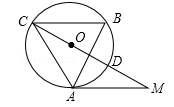
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
(年新疆、生产建设兵团)如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为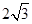 cm,且AB=6cm,求∠ACB.
cm,且AB=6cm,求∠ACB.