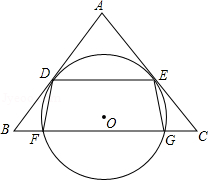
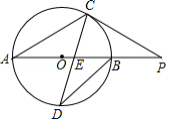
如图, 为 的直径, 为 上一点,经过点 的切线交 的延长线于点 , 交 的延长线于点 , 交 于 , 于 ,分别交 、 于 、 ,连接 , .
(1)求证: 平分 ;
(2)若 , ,
①求 的半径;
②求 的长.

如图,在 中, ,以 为直径的 与边 、 分别交于 、 两点,过点 作 ,垂足为点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
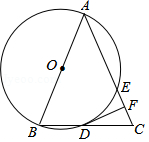
如图,已知 是 的直径, 为 上(异于 、 一点, 的切线 与 的延长线交于点 ; 为 上一点, 的延长线交 于点 , 为 上一点且 , 的延长线交 于点 .
(1)求证: ;
(2)若 、 的长是一元二次方程 的两根,求 的长;
(3)若 , ,求 的长.
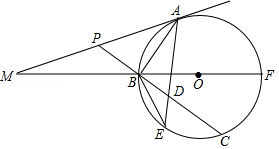
(材料阅读)
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1中的 .人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角 的大小是变化的.
(实际应用)
观测点 在图1所示的 上,现在利用这个工具尺在点 处测得 为 ,在点 所在子午线往北的另一个观测点 ,用同样的工具尺测得 为 . 是 的直径, .
(1)求 的度数;
(2)已知
,求这两个观测点之间的距离即
上
的长.
取

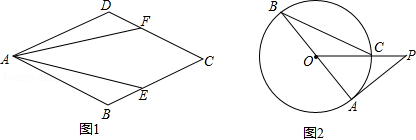
(1)如图1,在菱形 中, ,求证: .
(2)如图2, 是 的直径, 与 相切于点 , 与 相交于点 ,连接 , ,求 的度数.
已知: 为 的直径,延长 到点 ,过点 作圆 的切线,切点为 ,连接 ,且 .
(1)求 的度数;
(2)若点 是弧 的中点,连接 交 于点 ,且 ,求 的面积. 取
如图,在平面直角坐标系中,已知点 ,以原点 为圆心、3为半径作圆. 从点 出发,以每秒1个单位的速度沿 轴正半轴运动,运动时间为 .连接 ,将 沿 翻折,得到 .求 有一边所在直线与 相切时 的值.

如图,在平面直角坐标系中,已知点 ,以原点 为圆心、3为半径作圆. 从点 出发,以每秒1个单位的速度沿 轴正半轴运动,运动时间为 .连接 ,将 沿 翻折,得到 .求 有一边所在直线与 相切时 的值.

如图, 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,求弦 的长.

如图1,以 的边 为直径的 交边 于点 ,过点 作 的切线交 于点 ,且 .
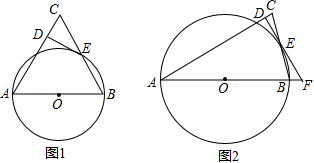
(1)试判断 的形状,并说明理由;
(2)如图2,若线段 、 的延长线交于点 , , ,求 的半径和 的长.
如图,在四边形 中, , , ,以点 为圆心, 为半径的圆与 相切于点 ,交 于点
(1)求 的大小及 的长度;
(2)在 的延长线上取一点 ,使得 上的一个动点 到点 的最短距离为 ,求 的长.

如图, 是 内一点, 与 相交于 、 两点,且与 、 分别相切于点 、 , ,连接 、 .
(1)求证: .
(2)已知 , ,求四边形 是矩形时 的半径.