如图,在四边形中,
,对角线
的垂直平分线与边
、
分别相交于点
、
.
(1)求证:四边形是菱形;
(2)若,
,求菱形
的周长.

如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=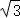 ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)

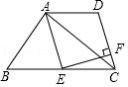
如图,在四边形 中, , 是 的中点, , , 于点 .
(1)求证:四边形 是菱形;
(2)若 , ,求 的长.
能够完全重合的平行四边形纸片 和 按图①方式摆放,其中 , .点 , 分别在边 , 上, 与 相交于点 .
【探究】求证:四边形 是菱形.
【操作一】固定图①中的平行四边形纸片 ,将平行四边形纸片 绕着点 顺时针旋转一定的角度,使点 与点 重合,如图②.则这两张平行四边形纸片未重叠部分图形的周长和为 .
【操作二】将图②中的平行四边形纸片 绕着点 继续顺时针旋转一定的角度,使点 与点 重合,连接 , ,如图③,若 ,则四边形 的面积为 .

如图,在四边形 中, 与 相交于点 ,且 ,点 在 上,满足 .
(1)求证:四边形 是平行四边形;
(2)若 , , ,求四边形 的面积.

如图,在菱形 中,将对角线 分别向两端延长到点 和 ,使得 .连接 , , , .
求证:四边形 是菱形.

如图,在平行四边形 中, 、 分别是 、 的中点, ,垂足为 , ,垂足为 , 与 相交于点 .
(1)证明: .
(2)若 ,求四边形 的对角线 的长.
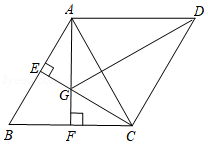
如图,在 中, 于点O,交BC于点E, , 交DE于点F,连接 ,点H为线段 上一点,连接 .
(1)判断四边形 的形状,并说明理由;
(2)当 时,求证: .
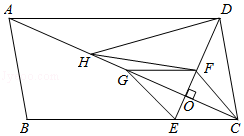
如图,在 中, , , , 、 分别是斜边 、直角边 上的点,把 沿着直线 折叠.

(1)如图1,当折叠后点 和点 重合时,用直尺和圆规作出直线 ;(不写作法和证明,保留作图痕迹)
(2)如图2,当折叠后点 落在 边上点 处,且四边形 是菱形时,求折痕 的长.
菱形 的对角线 , 相交于点 , ,点 是射线 上一个动点,过点 作 交射线 于点 ,以 , 为邻边作矩形 .

(1)如图1,当点 在线段 上时,求证: ;
(2)若延长 与边 交于点 ,将 沿直线 翻折 得到 .
①如图2,当点 在 上时,求证:四边形 为正方形;
②如图3,当 为定值 时,设 , 为大于0的常数,当且仅当 时,点 在矩形 的外部,求 的值.
如图,已知在中,
,
,
分别是
,
,
的中点,连结
,
,
.
(1)求证:四边形是平行四边形;
(2)若,
,求四边形
的周长.

如图,将沿着
边翻折,得到
,且
.
(1)判断四边形的形状,并说明理由;
(2)若,
,求四边形
的面积.

如图,矩形中,
,
,点
是对角线
的中点,过点
的直线分别交
、
边于点
、
.
(1)求证:四边形是平行四边形;
(2)当时,求
的长.

如图,在 中, , 、 分别是边 、 的中点,过点 作 交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若四边形 的面积为24, ,求 的长.
