菱形 的对角线 , 相交于点 , ,点 是射线 上一个动点,过点 作 交射线 于点 ,以 , 为邻边作矩形 .
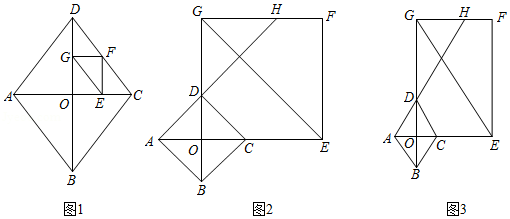
(1)如图1,当点 在线段 上时,求证: ;
(2)若延长 与边 交于点 ,将 沿直线 翻折 得到 .
①如图2,当点 在 上时,求证:四边形 为正方形;
②如图3,当 为定值 时,设 , 为大于0的常数,当且仅当 时,点 在矩形 的外部,求 的值.
推荐套卷
菱形 的对角线 , 相交于点 , ,点 是射线 上一个动点,过点 作 交射线 于点 ,以 , 为邻边作矩形 .

(1)如图1,当点 在线段 上时,求证: ;
(2)若延长 与边 交于点 ,将 沿直线 翻折 得到 .
①如图2,当点 在 上时,求证:四边形 为正方形;
②如图3,当 为定值 时,设 , 为大于0的常数,当且仅当 时,点 在矩形 的外部,求 的值.