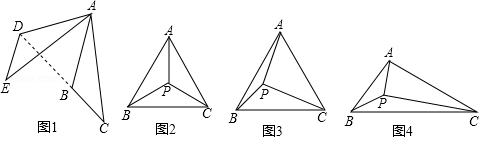
如图,在 中, , ,点 为 中点,点 为直线 上的动点(不与点 、点 重合),连接 、 ,将线段 绕点 顺时针旋转 ,得到线段 ,连接 .
(1)如图1,当点 在线段 上时,请直接写出线段 与 的数量关系.
(2)如图2,当点 在 延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点
在
延长线上时,若
,
,请求出
的长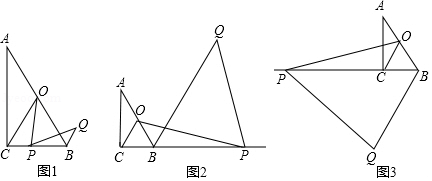
如图1,在 中, , ,点 、 分别在 、 边上, ,连接 、 、 ,点 、 、 分别是 、 、 的中点,连接 、 、 .

(1) 与 的数量关系是 ;
(2)将 绕点 逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
(3)若 , ,在将图1中的 绕点 逆时针旋转一周的过程中,当 、 、 三点在一条直线上时, 的长度为 .
如图, 在平面直角坐标系内,顶点的坐标分别为 , , .
(1)平移 ,使点 移动到点 ,画出平移后的△ ,并写出点 , 的坐标.
(2)画出 关于原点 对称的△ .
(3)线段 的长度为 .

思维启迪:
(1)如图1, , 两点分别位于一个池塘的两端,小亮想用绳子测量 , 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达 点的点 ,连接 ,取 的中点 (点 可以直接到达 点),利用工具过点 作 交 的延长线于点 ,此时测得 米,那么 , 间的距离是 200 米.
思维探索:
(2)在 和 中, , ,且 , ,将 绕点 顺时针方向旋转,把点 在 边上时 的位置作为起始位置(此时点 和点 位于 的两侧),设旋转角为 ,连接 ,点 是线段 的中点,连接 , .
①如图2,当 在起始位置时,猜想: 与 的数量关系和位置关系分别是 ;
②如图3,当 时,点 落在 边上,请判断 与 的数量关系和位置关系,并证明你的结论;
③当 时,若 , ,请直接写出 的值.

如图,在矩形 中, 是 的中点,连接 、 .
(1)求证: ;
(2)若 , ,求 的周长.

如图,在 中, 于 , , , , 分别是 , 的中点.
(1)求证: , ;
(2)连接 ,若 ,求 的长.

在 中, , , ,若 ,如图1,则有 ;若 为锐角三角形时,小明猜想: ,理由如下:如图2,过点 作 于点 ,设 .在 中, ,在 中,
,
当 为锐角三角形时,
所以小明的猜想是正确的.
(1)请你猜想,当 为钝角三角形时, 与 的大小关系.
(2)温馨提示:在图3中,作 边上的高.
(3)证明你猜想的结论是否正确.

如图,直角 中, 为直角, , .点 , , 分别在 , , 边上同时开始作匀速运动,2秒后三个点同时停止运动,点 由点 出发以每秒3个单位的速度向点 运动,点 由点 出发以每秒5个单位的速度向点 运动,点 由点 出发以每秒4个单位的速度向点 运动,在运动过程中:
(1)求证: , , 的面积相等;
(2)求 面积的最小值;
(3)用 (秒 表示运动时间,是否存在 ,使 ?若存在,请直接写出 的值;若不存在,请说明理由.

在Rt△ABC中, ,点D为斜边AB的中点, , ,过点A作 且 ,过点E作EF垂直于AC边所在的直线,垂足为点F,连接DF,请你画出图形,并直接写出线段DF的长.
在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,△ ABC的三个顶点均在格点上,以点 A为圆心的  与 BC相切于点 D,分别交 AB、 AC于点 E、 F.
与 BC相切于点 D,分别交 AB、 AC于点 E、 F.
(1)求△ ABC三边的长;
(2)求图中由线段 EB、 BC、 CF及  所围成的阴影部分的面积.
所围成的阴影部分的面积.

如图,等边△ ABC中, AB=6,点 D在 BC上, BD=4,点 E为边 AC上一动点(不与点 C重合),△ CDE关于 DE的轴对称图形为△ FDE.
(1)当点 F在 AC上时,求证: DF∥ AB;
(2)设△ ACD的面积为 S 1,△ ABF的面积为 S 2,记 S= S 1﹣ S 2, S是否存在最大值?若存在,求出 S的最大值;若不存在,请说明理由;
(3)当 B, F, E三点共线时.求 AE的长.

如图,在四边形 ABCD中,∠ B=60°,∠ D=30°, AB= BC.
(1)求∠ A+∠ C的度数;
(2)连接 BD,探究 AD, BD, CD三者之间的数量关系,并说明理由;
(3)若 AB=1,点 E在四边形 ABCD内部运动,且满足 AE 2= BE 2+ CE 2,求点 E运动路径的长度.

如图,△ ACE内接于⊙ O, AB是⊙ O的直径,弦 CD⊥ AB于点 H,交 AE于点 F,过点 E作 EG∥ AC,分别交 CD、 AB的延长线于点 G、 M.
(1)求证:△ ECF∽△ GCE;
(2)若tan G= , AH=3 ,求⊙ O半径.

(1)【操作发现】
如图1,将△ ABC绕点 A顺时针旋转60°,得到△ ADE,连接 BD,则∠ ABD= 度.
(2)【类比探究】
如图2,在等边三角形 ABC内任取一点 P,连接 PA, PB, PC,求证:以 PA, PB, PC的长为三边必能组成三角形.
(3)【解决问题】
如图3,在边长为 的等边三角形 ABC内有一点 P,∠ APC=90°,∠ BPC=120°,求△ APC的面积.
(4)【拓展应用】
如图4是 A, B, C三个村子位置的平面图,经测量 AC=4, BC=5,∠ ACB=30°, P为△ ABC内的一个动点,连接 PA, PB, PC.求 PA+ PB+ PC的最小值.